
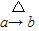 (f(x),g(x)).若
(f(x),g(x)).若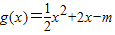 ,且
,且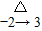 (f(x),g(x))=
(f(x),g(x))=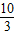 ,求m的值.
,求m的值.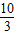 ,故要利用导数求出F(x)=f(x)-g(x)的最大值与最小值,由于不知那一个的绝对值最大,故可以讨论建立方程,求出参数的值即可.
,故要利用导数求出F(x)=f(x)-g(x)的最大值与最小值,由于不知那一个的绝对值最大,故可以讨论建立方程,求出参数的值即可.
 ,b=0;
,b=0; x3-
x3-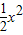 -2x+m
-2x+m +m,F(-1)=
+m,F(-1)=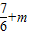 ,F(2)=-
,F(2)=-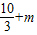 ,F(3)=-
,F(3)=-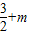
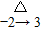 (f(x),g(x))=
(f(x),g(x))=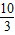 ,
,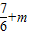 |=
|=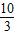 (m>0)或|-
(m>0)或|-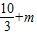 |=
|=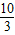 (m<0)
(m<0)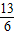


科目:高中数学 来源: 题型:
| π | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | -0.61 | -0.59 | -0.56 | -0.35 | 0 | 0.26 | 0.42 | 1.57 | 3.27 |
| y | 0.07 | 0.02 | -0.03 | -0.22 | 0 | 0.21 | 0.20 | -10.04 | -101.63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com