Question

【题目】里约热内卢奥运会正在如火如荼的进行，奥运会纪念品销售火爆，已知某种纪念品的单价是5元，买x（x∈{1,2,3,4,5}）件该纪念品需要y元．试用函数的三种表示法表示函数y＝f（x）．

Answer 1

【答案】0、解：这个函数的定义域是数集{1,2,3,4,5}，
用解析法可将函数y＝f（x）表示为y＝5x，x∈{1,2,3,4,5}．
用列表法可将函数y＝f（x）表示为

纪念品件数x	1	2	3	4	5
钱数y	5	10	15	20	25

用图象法可将函数y＝f（x）表示如图．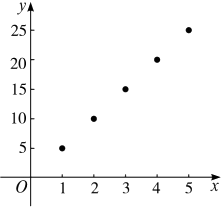

【解析】实际问题中的函数表示,用三种表示方法:解析式法,数表法,图象法.
【考点精析】认真审题，首先需要了解函数的表示方法(函数的三种表示方法解析法：就是用数学表达式表示两个变量之间的对应关系;列表法：就是列出表格来表示两个变量之间的对应关系;图象法：就是用图象表示两个变量之间的对应关系)，还要掌握函数图象的作法(图象的作法与平移：①据函数表达式，列表、描点、连光滑曲线；②利用熟知函数的图象的平移、翻转、伸缩变换；③利用反函数的图象与对称性描绘函数图象)的相关知识才是答题的关键．