Question

已知△ABC的三边长分别是3、4、5,点P是它的内切圆上一点,求以PA、PB、PC分别为直径的三个圆面积之和的最大值和最小值.

Answer 1

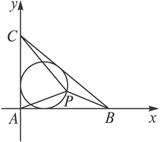
解析:由已知得△ABC为直角三角形,建立如下图所示的直角坐标系,则A(0,0)、B(4,0)、C(0,3).

设内切圆半径为r,则r=(a+b-c)=1,故内切圆的方程为(x-1)²+(y-1)²=1.

又设P点坐标为(1+cosα,1+sinα),以PA、PB、PC为直径的三个圆面积

S=π()²+π()²+π()²

=(PA²+PB²+PC²)

=［(1+cosα)²+(1+sinα)²+(1+cosα-4)²+(1+sinα)²+(1+cosα)²+(1+sinα-3)²］

= (10-cosα),

又∵-1≤cosα≤1,∴当cosα=-1时,S_max=;当cosα=1时,S_min=.