
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点.
(1)证明:BC1//平面A1CD;
(2)设AA1=AC=CB=2,AB= ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:解答题
如图,三棱柱ABC—A1B1C1的侧面AA1B1B为正方形,侧面BB1C1C为菱形,∠CBB1=60°,AB⊥B1C.
(1)求证:平面AA1B1B⊥平面BB1C1C;
(2)若AB=2,求三棱柱ABC—A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1, ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(1)若 ,求证:
,求证: ;
;
(2)若二面角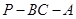 的大小为
的大小为 ,则CE为何值时,三棱锥
,则CE为何值时,三棱锥 的体积为
的体积为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图在四棱锥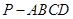 中,底面
中,底面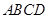 是矩形,
是矩形,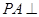 平面
平面 ,
,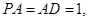
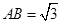 ,点
,点 是
是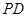 中点,点
中点,点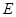 是
是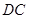 边上的任意一点.
边上的任意一点.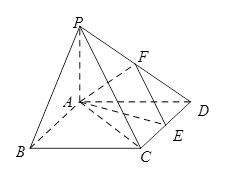
(1)当点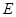 为
为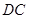 边的中点时,判断
边的中点时,判断 与平面
与平面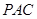 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)证明:无论点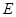 在
在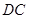 边的何处,都有
边的何处,都有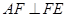 ;
;
(3)求三棱锥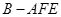 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥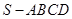 的底面是正方形,侧棱
的底面是正方形,侧棱 底面
底面 ,过
,过 作
作 垂直
垂直 交
交 于
于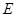 点,作
点,作 垂直
垂直 交
交 于
于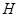 点,平面
点,平面 交
交 于
于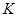 点,且
点,且 ,
, .
.
(1)试证明不论点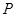 在何位置,都有
在何位置,都有 ;
;
(2)求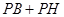 的最小值;
的最小值;
(3)设平面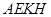 与平面
与平面 的交线为
的交线为 ,求证:
,求证: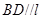 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,一简单组合体的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC 平面ABC.
平面ABC.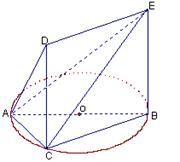
(1)证明:平面ACD 平面
平面 ;
;
(2)若 ,
, ,
, ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com