
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() 满足,
满足,![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,则满足
,则满足![]() 的最小的
的最小的![]() 值为______.
值为______.
【答案】7
【解析】
根据题意,将Sn=3an﹣2变形可得Sn﹣1=3an﹣1﹣2,两式相减变形,并令n=1求出a1的值,即可得数列{an}是等比数列,求得数列{an}的通项公式,再由错位相减法求出Tn的值,利用Tn>100,验证分析可得n的最小值,即可得答案.
根据题意,数列{an}满足Sn=3an﹣2,①
当n≥2时,有Sn﹣1=3an﹣1﹣2,②,
①﹣②可得:an=3an﹣3an﹣1,变形可得2an=3an﹣1,
当n=1时,有S1=a1=3a1﹣2,解可得a1=1,
则数列{an}是以a1=1为首项,公比为![]() 的等比数列,则an=(
的等比数列,则an=(![]() )n﹣1,
)n﹣1,
数列{nan}的前n项和为Tn,则Tn=1+2![]() 3×(
3×(![]() )2+……+n×(
)2+……+n×(![]() )n﹣1,③
)n﹣1,③
则有![]() Tn
Tn![]() 2×(
2×(![]() )2+3×(
)2+3×(![]() )3+……+n×(
)3+……+n×(![]() )n,④
)n,④
③﹣④可得:![]() Tn=1+(
Tn=1+(![]() )+(
)+(![]() )2+……×(
)2+……×(![]() )n﹣1﹣n×(
)n﹣1﹣n×(![]() )n=﹣2(1
)n=﹣2(1![]() )﹣n×(
)﹣n×(![]() )n,
)n,
变形可得:Tn=4+(2n﹣4)×(![]() )n,
)n,
若Tn>100,即4+(2n﹣4)×(![]() )n>100,
)n>100,
分析可得:n≥7,故满足Tn>100的最小的n值为7;
故答案为:7.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某水果种植基地引进一种新水果品种,经研究发现该水果每株的产量![]() (单位:
(单位:![]() )和与它“相近”的株数
)和与它“相近”的株数![]() 具有线性相关关系(两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
),并分别记录了相近株数为0,1,2,3,4时每株产量的相关数据如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出该种水果每株的产量![]() 关于它“相近”株数
关于它“相近”株数![]() 的回归方程;
的回归方程;
(2)有一种植户准备种植该种水果500株,且每株与它“相近”的株数都为![]() ,计划收获后能全部售出,价格为10元
,计划收获后能全部售出,价格为10元![]() ,如果收入(收入=产量×价格)不低于25000元,则
,如果收入(收入=产量×价格)不低于25000元,则![]() 的最大值是多少?
的最大值是多少?
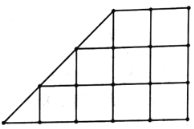
(3)该种植基地在如图所示的直角梯形地块的每个交叉点(直线的交点)处都种了一株该种水果,其中每个小正方形的边长和直角三角形的直角边长都为![]() ,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
,已知该梯形地块周边无其他树木影响,若从所种的该水果中随机选取一株,试根据(1)中的回归方程,预测它的产量的分布列与数学期望.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为: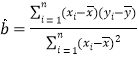 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市面上有某品牌![]() 型和
型和![]() 型两种节能灯,假定
型两种节能灯,假定![]() 型节能灯使用寿命都超过5000小时,经销商对
型节能灯使用寿命都超过5000小时,经销商对![]() 型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:
型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:

某商家因原店面需要重新装修,需租赁一家新店面进行周转,合约期一年.新店面需安装该品牌节能灯5支(同种型号)即可正常营业.经了解,![]() 型20瓦和
型20瓦和![]() 型55瓦的两种节能灯照明效果相当,都适合安装.已知
型55瓦的两种节能灯照明效果相当,都适合安装.已知![]() 型和
型和![]() 型节能灯每支的价格分别为120元、25元,当地商业电价为0.75元/千瓦时.假定该店面一年周转期的照明时间为3600小时,若正常营业期间灯坏了立即购买同型灯管更换.(用频率估计概率)
型节能灯每支的价格分别为120元、25元,当地商业电价为0.75元/千瓦时.假定该店面一年周转期的照明时间为3600小时,若正常营业期间灯坏了立即购买同型灯管更换.(用频率估计概率)
(Ⅰ)根据频率直方图估算![]() 型节能灯的平均使用寿命;
型节能灯的平均使用寿命;
(Ⅱ)根据统计知识知,若一支灯管一年内需要更换的概率为![]() ,那么
,那么![]() 支灯管估计需要更换
支灯管估计需要更换![]() 支.若该商家新店面全部安装了
支.若该商家新店面全部安装了![]() 型节能灯,试估计一年内需更换的支数;
型节能灯,试估计一年内需更换的支数;
(Ⅲ)若只考虑灯的成本和消耗电费,你认为该商家应选择哪种型号的节能灯,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() 、
、![]() 和
和![]() 所在直线上的动点:
所在直线上的动点:

(1)求![]() 的取值范围:
的取值范围:
(2)若![]() 为面
为面![]() 内的一点,且
内的一点,且![]() ,
,![]() ,求
,求![]() 的余弦值:
的余弦值:
(3)若![]() 、
、![]() 分别是所在正方形棱的中点,试问在棱
分别是所在正方形棱的中点,试问在棱![]() 上能否找到一点
上能否找到一点![]() ,使
,使![]() 平面
平面![]() ?若能,试确定点
?若能,试确定点![]() 的位置,若不能,请说明理由.
的位置,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切,圆心在
相切,圆心在![]() 轴上,且直线
轴上,且直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率乘积为
的斜率乘积为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1的方程为![]() ,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,O为坐标原点.
,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,O为坐标原点.
(1)求双曲线C2的方程;
(2)若直线l:y=kx+![]() 与双曲线C2恒有两个不同的交点A和B,且
与双曲线C2恒有两个不同的交点A和B,且![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不等式组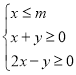 表示的平面区域为D,
表示的平面区域为D,![]() 的最大值等于8.
的最大值等于8.
(1)求![]() 的值;
的值;
(2)求![]() 的取值范围;
的取值范围;
(3)若直线![]() 过点P(-3,3),求区域D在直线
过点P(-3,3),求区域D在直线![]() 上的投影的长度的取值范围.
上的投影的长度的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com