
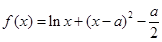 ,
,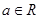 .
. 在
在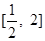 上单调递增,求实数
上单调递增,求实数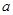 的取值范围;
的取值范围; 的极值点.
的极值点.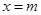 为函数
为函数 的极小值点,
的极小值点,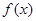 的图象与
的图象与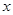 轴交于
轴交于 两点,且
两点,且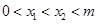 ,
,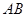 中点为
中点为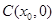 ,
,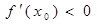 .
.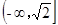 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.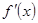 ,在
,在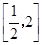 上
上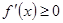 恒成立,反解参数
恒成立,反解参数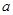 ,转化成
,转化成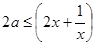 恒成立问题,利用基本不等式求
恒成立问题,利用基本不等式求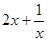 的最小值问题;
的最小值问题;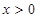 ,所以设
,所以设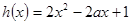 ,分情况讨论
,分情况讨论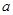 在不同情况下,
在不同情况下,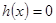 的根,通过
的根,通过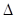 来讨论,主要分
来讨论,主要分 以及
以及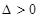 的情况,求出导数为0的值,判断两侧的单调性是否改变,从而确定极值点;
的情况,求出导数为0的值,判断两侧的单调性是否改变,从而确定极值点;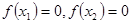 ,两式相减,结合中点坐标公式,
,两式相减,结合中点坐标公式,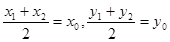 ,表示出
,表示出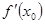 ,设出
,设出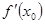 的能表示正负的部分函数,再求导数,利用导数得出单调性,从而确定
的能表示正负的部分函数,再求导数,利用导数得出单调性,从而确定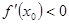 .
.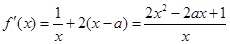
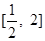 上不等式
上不等式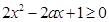 恒成立.
恒成立.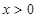 ,所以
,所以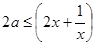 .所以
.所以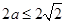 ,
,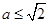
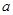 的取值范围是
的取值范围是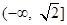 . 2分
. 2分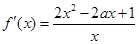 ,令
,令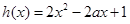
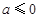 时,在
时,在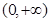 上
上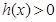 恒成立,这时
恒成立,这时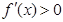 ,此时,函数
,此时,函数 没有极值点; ..3分
没有极值点; ..3分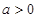 时,
时,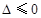 ,即
,即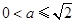 时,在
时,在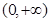 上
上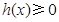 恒成立,这时
恒成立,这时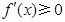 ,此时,函数
,此时,函数 没有极值点; .4分
没有极值点; .4分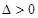 ,即
,即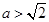 时,
时,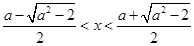 时,
时,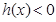 ,这时
,这时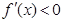 ;
;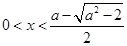 或
或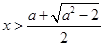 时,
时,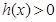 ,这时
,这时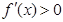 ;
;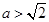 时,
时,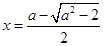 是函数
是函数 的极大值点;
的极大值点;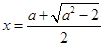 是函数
是函数 的极小值点.
的极小值点.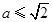 时,函数
时,函数 没有极值点; .6分
没有极值点; .6分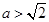 时,
时,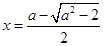 是函数
是函数 的极大值点;
的极大值点;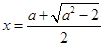 是函数
是函数 的极小值点. 8分
的极小值点. 8分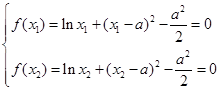 两式相减,
两式相减,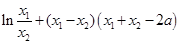 ①
①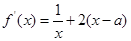 ,得
,得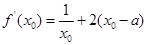 ②得①代入②,得
②得①代入②,得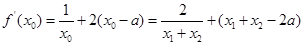
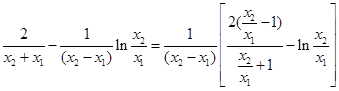 10分
10分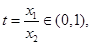 且
且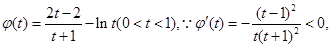
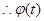 在
在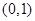 上递减,
上递减,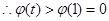
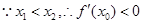 12分
12分

 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com