
【题目】如图,四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(3)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
![]() 取AB中点O,推导出
取AB中点O,推导出![]() ,
,![]() ,
,![]() ,从而
,从而![]() 平面ABCD,进而
平面ABCD,进而![]() ,再求出
,再求出![]() ,从而
,从而![]() 平面AED,由此能证明平面
平面AED,由此能证明平面![]() 平面AED;
平面AED;![]() 过A作
过A作![]() 于点G,则
于点G,则![]() 即为直线AB与平面BED所成的角,由此能求出直线AB与平面BED所成角的正弦值;
即为直线AB与平面BED所成的角,由此能求出直线AB与平面BED所成角的正弦值;![]() 3
3![]() 二面角
二面角![]() 的平面角与二面角
的平面角与二面角![]() 的平面角互补,从而问题转化为求二面角
的平面角互补,从而问题转化为求二面角![]() 的正弦值,过A作
的正弦值,过A作![]() 于点G,过A作
于点G,过A作![]() 于点H,则
于点H,则![]() 即为二面角
即为二面角![]() 的平面角,由此能求出二面角
的平面角,由此能求出二面角![]() 的正弦值.
的正弦值.
(1)证明:取![]() 中点
中点![]() ,
,
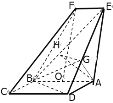
易知四边形![]() 是平行四边形,
是平行四边形,
则![]() 又
又![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
又![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]()
在![]() 中,由
中,由![]()
得![]() ,
,
∴![]()
∴![]() ,又
,又![]() ,
,
∴![]() 面
面![]()
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]()
(2)过![]() 作
作![]() 于点
于点![]() ,
,

由(1)知![]() 平面
平面![]() ,
,
则![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角
所成的角
又![]()
∴![]()
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
(3)∵二面角![]() 的平面角与二面角
的平面角与二面角![]() 的平面角互补,
的平面角互补,
∴问题转化为求二面角![]() 的正弦值
的正弦值
过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,

由(1)知![]() 即切二面角
即切二面角![]() 的平面角
的平面角
∵![]() ∴
∴![]()
又![]() ∴
∴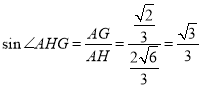
∴二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
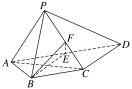
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产基地有五台机器,现有五项工作待完成,每台机器完成每项工作后获得的效益值如表所示.若每台机器只完成一项工作,且完成五项工作后获得的效益值总和最大,则下列叙述错误的的是_____________.
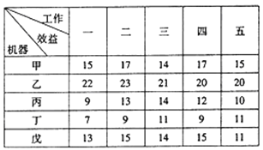
①甲只能承担第四项工作
②乙不能承担第二项工作
③丙可以不承担第三项工作
④丁可以承担第三项工作
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)直接写出![]() 的零点;
的零点;
(2)在坐标系中,画出![]() 的示意图(注意要画在答题纸上)
的示意图(注意要画在答题纸上)
(3)根据图象讨论关于![]() 的方程
的方程![]() 的解的个数:
的解的个数:
(4)若方程![]() ,有四个不同的根
,有四个不同的根![]() 、
、![]() 、
、![]() 、
、![]() 直接写出这四个根的和;
直接写出这四个根的和;
(5)若函数![]() 在区间
在区间![]() 上既有最大值又有最小值,直接写出a的取值范围.
上既有最大值又有最小值,直接写出a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在含有![]() 个元素的集合
个元素的集合![]() 中,若这
中,若这![]() 个元素的一个排列(
个元素的一个排列(![]() ,
,![]() ,…,
,…,![]() )满足
)满足![]() ,则称这个排列为集合
,则称这个排列为集合![]() 的一个错位排列(例如:对于集合
的一个错位排列(例如:对于集合![]() ,排列
,排列![]() 是
是![]() 的一个错位排列;排列
的一个错位排列;排列![]() 不是
不是![]() 的一个错位排列).记集合
的一个错位排列).记集合![]() 的所有错位排列的个数为
的所有错位排列的个数为![]() .
.
(1)直接写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)当![]() 时,试用
时,试用![]() ,
,![]() 表示
表示![]() ,并说明理由;
,并说明理由;
(3)试用数学归纳法证明:![]() 为奇数.
为奇数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系.
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程![]() 的回归系数a,b;
的回归系数a,b;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com