
【题目】已知点A、B、C、D的坐标分别为A(3,0)、B(0,3)、C(cosα,sinα),![]() ,α∈(
,α∈(![]() ,
,![]() ).
).
(1)若![]() ,求角α的值;
,求角α的值;
(2)若![]() ,求
,求![]() 的值.
的值.
(3)若![]() 在定义域α∈(
在定义域α∈(![]() ,
,![]() )有最小值
)有最小值![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用向量的坐标运算与向量的模![]() ,可求得sinα=cosα,从而可求得角α的值;
,可求得sinα=cosα,从而可求得角α的值;
(2)由![]() 可求得sinα+cosα=
可求得sinα+cosα=![]() ,从而可求得sin2α,而
,从而可求得sin2α,而![]() 可化简为2sinαcosα,从而可得答案;
可化简为2sinαcosα,从而可得答案;
(3)依题意记y=f(α)=﹣2cos2α﹣tsinα﹣t2+2,令x=sinα,结合题意可求得y=2x2﹣tx﹣t2,x∈(﹣1,1),利用二次函数的单调性与最值即可求得t的值.
(1)∵![]() =(cosα﹣3,sinα),
=(cosα﹣3,sinα),![]() =(cosα,sinα﹣3),
=(cosα,sinα﹣3),
∴|![]() |=
|=![]() =
=![]() ,
,
|![]() |=
|=![]() =
=![]()
由|![]() |=|
|=|![]() |得sinα=cosα,又α∈(
|得sinα=cosα,又α∈(![]() ,
,![]() ),
),
∴α=![]()
(2)由![]()
![]() =﹣1得(cosα﹣3)cosα+sinα(sinα﹣3)=﹣1.∴sinα+cosα=
=﹣1得(cosα﹣3)cosα+sinα(sinα﹣3)=﹣1.∴sinα+cosα=![]() ,①
,①
又![]() =
=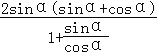 =2sinαcosα.
=2sinαcosα.
①式两边平方得1+2sinαcosα=![]() ,∴2sinαcosα=
,∴2sinαcosα=![]() .
.
∴![]() =﹣
=﹣![]() .
.
(3)依题意记y=f(α)=﹣2cos2α﹣tsinα﹣t2+2
=﹣2(1﹣sin2α)﹣tsinα﹣t2+2
=2sin2α﹣tsinα﹣t2
令x=sinα,∵α∈(![]() ,
,![]() ),∴sinα∈(﹣1,1),
),∴sinα∈(﹣1,1),
∴y=2x2﹣tx﹣t2,x∈(﹣1,1),其对称轴为x=![]() ,
,
∵y=2x2﹣tx﹣t2在x∈(﹣1,1)上存在最小值,∴对称轴x=![]() ∈(﹣1,1),
∈(﹣1,1),
∴t∈(﹣4,4),当且仅当x=![]() 时,y=2x2﹣tx﹣t2取最小值,为ymin=2×
时,y=2x2﹣tx﹣t2取最小值,为ymin=2×![]() ﹣t
﹣t![]() ﹣t2=﹣
﹣t2=﹣![]() t2=﹣1,
t2=﹣1,
∴t=±![]()


科目:高中数学 来源: 题型:
【题目】2017年10月18日至10月24日,中国共产党第十九次全国代表大会![]() 简称党的“十九大”
简称党的“十九大”![]() 在北京召开
在北京召开![]() 一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在
一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在![]() 内,按成绩分成5组:第1组
内,按成绩分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
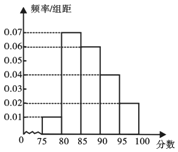
![]() 求这100人的平均得分
求这100人的平均得分![]() 同一组数据用该区间的中点值作代表
同一组数据用该区间的中点值作代表![]() ;
;
![]() 求第3,4,5组分别选取的作深入学习的人数;
求第3,4,5组分别选取的作深入学习的人数;
![]() 若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解![]() 市高三数学复习备考情况,该市教研机构组织了一次检测考试,并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.
市高三数学复习备考情况,该市教研机构组织了一次检测考试,并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.

(1)根据频率分布直方图,估计该市此次检测理科数学的平均成绩![]() ;(精确到个位)
;(精确到个位)
(2)研究发现,本次检测的理科数学成绩![]() 近似服从正态分布
近似服从正态分布![]() (
(![]() ,
, ![]() 约为19.3).
约为19.3).
![]() 按以往的统计数据,理科数学成绩能达到升一本分数要求的同学约占
按以往的统计数据,理科数学成绩能达到升一本分数要求的同学约占![]() ,据此估计本次检测成绩达到升一本的理科数学成绩大约是多少分?(精确到个位)
,据此估计本次检测成绩达到升一本的理科数学成绩大约是多少分?(精确到个位)
![]() 已知
已知![]() 市理科考生约有1000名,某理科学生此次检测数学成绩为107分,则该学生全市排名大约是多少名?
市理科考生约有1000名,某理科学生此次检测数学成绩为107分,则该学生全市排名大约是多少名?
(说明: ![]() 表示
表示![]() 的概率,
的概率, ![]() 用来将非标准正态分布化为标准正态分布,即
用来将非标准正态分布化为标准正态分布,即![]() ,从而利用标准正态分布表
,从而利用标准正态分布表![]() ,求
,求![]() 时的概率
时的概率![]() ,这里
,这里![]() .相应于
.相应于![]() 的值
的值![]() 是指总体取值小于
是指总体取值小于![]() 的概率,即
的概率,即![]() .参考数据:
.参考数据: ![]() ,
, ![]() ,
, ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,左顶点
,左顶点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若以
两点,若以![]() 为直径的圆经过坐标原点,证明:点
为直径的圆经过坐标原点,证明:点![]() 到直线
到直线![]() 的距离为定值;
的距离为定值;
(III)在(Ⅱ)的条件下,试求![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 的公比为q,等差数列
的公比为q,等差数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 的公差为d,且q≠1,d≠0.记
的公差为d,且q≠1,d≠0.记![]() (
(![]() 1,2,3,4).
1,2,3,4).
(1)求证:数列![]() ,
, ![]() ,
, ![]() 不是等差数列;
不是等差数列;
(2)设![]() ,q=2.若数列
,q=2.若数列![]() ,
, ![]() ,
, ![]() 是等比数列,求
是等比数列,求![]() 关于d的函数关系式及其定义域;
关于d的函数关系式及其定义域;
(3)数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 能否为等比数列?并说明理由.
能否为等比数列?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com