
【题目】已知向量![]() ,函数
,函数![]() 的最小值为
的最小值为![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() ;
;
(3)已知函数![]() 为定义在上的增函数,且对任意的
为定义在上的增函数,且对任意的![]() 都满足
都满足![]() ,问:是否存在这样的实数
,问:是否存在这样的实数![]() ,使不等式
,使不等式![]() 对所有
对所有![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)数![]() 的最小值为
的最小值为![]() .利用向量的乘积运算求出
.利用向量的乘积运算求出![]() 的解析式,求出最小值可得
的解析式,求出最小值可得![]() ,当
,当![]() 时,可得
时,可得![]() 的值;
的值;
(2)根据对称轴,讨论参数的范围分段表示求![]() ;
;
(3)假设存在符合条件的实数![]() ,则依题意有
,则依题意有![]() ,对所有θ
,对所有θ![]() 恒成立.设
恒成立.设![]() ,则
,则![]() ,利用三角函数的有界限转化为勾勾函数的求最值问题,利用不等式的性质即可求出
,利用三角函数的有界限转化为勾勾函数的求最值问题,利用不等式的性质即可求出![]() 的取值范围.
的取值范围.
详解:
![]()
(1)设![]() ,则
,则![]()
当![]() 时,
时,![]() 在
在![]() 为减函数,
为减函数,
所以![]() 时取最小值
时取最小值![]() .
.
(2)![]() ,
,![]() ,其对称轴为
,其对称轴为![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() ;
;
综上,![]()
(3)假设存在符合条件的实数![]() ,则依题意有
,则依题意有![]() ,
,
对所有![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,
,
∴![]() ,
,![]() 恒成立
恒成立
即![]() ,
,![]() 恒成立,
恒成立,
∵![]() ,
,
∴![]()
∴![]() ,
,![]() 恒成立
恒成立
令![]()
由![]() 在
在![]() 上单调递增
上单调递增
则![]()
∴![]()
所以存在符合条件的实数![]() ,并且
,并且![]() 的取值范围为
的取值范围为![]() ..
..


科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足
满足![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() .
.
(1)若数列![]() 是首项为正数,公比为
是首项为正数,公比为![]() 的等比数列.
的等比数列.
①求证:数列![]() 为等比数列;
为等比数列;
②若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)已知![]() 为递增数列,即
为递增数列,即![]() .若对任意
.若对任意![]() ,数列
,数列![]() 中都存在一项
中都存在一项![]() 使得
使得![]() ,求证:数列
,求证:数列![]() 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,△PAD为正三角形,平面PAD⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB=2AD=4.

(1)求证:平面PCD⊥平面PAD;
(2)求三棱锥P—ABC的体积;
(3)在棱PC上是否存在点E,使得BE∥平面PAD?若存在,
请确定点E的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 。
。
(Ⅰ)求证:直线![]() 与圆C恒有两个交点;
与圆C恒有两个交点;
(Ⅱ)求出直线![]() 被圆C截得的最短弦长,并求出截得最短弦长时的
被圆C截得的最短弦长,并求出截得最短弦长时的![]() 的值;
的值;
(Ⅲ)设直线![]() 与圆C的两个交点为M,N,且
与圆C的两个交点为M,N,且![]() (点C为圆C的圆心),求直线
(点C为圆C的圆心),求直线![]() 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,且该几何体的体积是3,则正视图的![]() 的值__________.
的值__________.

【答案】3
【解析】 由已知中的三视图可得该几何体是一个以直角梯形为底面,梯形上下边长为![]() 和
和![]() ,高为
,高为![]() ,
,
如图所示, ![]() 平面
平面![]() ,
,
所以底面积为![]() ,
,
几何体的高为![]() ,所以其体积为
,所以其体积为![]() .
.

点睛:在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何体实际形状时,一般是以正视图和俯视图为主,结合侧视图进行综合考虑.求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解.
【题型】填空题
【结束】
16
【题目】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,
, ![]() 为直线
为直线![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
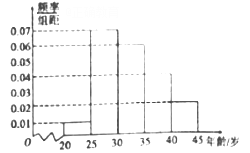
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,a4=2且![]() ,数列
,数列![]() 满足
满足![]()
![]() ,
,
(1)证明:数列{an}为等差数列;
(2)是否存在正整数![]() ,
,![]() (1<
(1<![]() ),使得
),使得![]() 成等比数列,若存在,求出
成等比数列,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图,则下面结论中不正确的是( )


建设前经济收入构成比例 建设后经济收入构成比例
A. 新农村建设后,养殖收入增加了一倍
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,种植收入减少
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com