解:(I)(1)∵
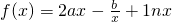
,∴

.(1分)
∵f(x)在x=1,x=

处取得极值,∴
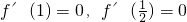
(2分)
即
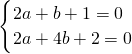
解得
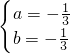
∴所求a、b的值分别为-
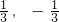
(4分)
(ii)在
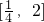
存在x
o,使得不等式f(xo)-c≤0成立,只需c≥[f(x)]min,
由
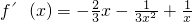
=
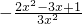
=

,
∴

时,f'(x)<0,故f(x)在
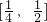
是单调递减;
当
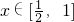
时,f'(x)>0,故f(x)在

是单调递增;
当x∈[1,2]时,f'(x)<0,故f(x)在[1,2]是单调递减;
∴

是f(x)在
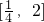
上的极小值.(6分)
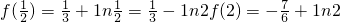
,
且
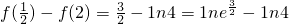
,
又e
3-16>0,∴

,
∴[f(x)]min=f(2),∴
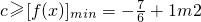
,∴c的取值范围为
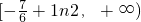
,
所以c的最小值为-
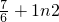
.(9分)
(Ⅱ)当a=b时,f'(x)=
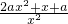
,
①当a=0时,f(x)=1nx.则f(x)在(0,+∞)上单调递增;
②当a>0时,∵x>0,∴2ax2+x+a>0,∴f'(x)>0,则f(x)在(0,+∞)上单调递增;
③当a<0时,设g(x)=2ax2+x+a,只需△≤0,从面得
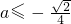
,此时f(x)在(0+∞)上单调递减;
综上得,a的取值范围是

.(14分)
分析:(I)(i)先对函数进行求导,根据函数在
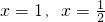
取得极值,则
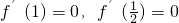
,代入可求a,b的值.
(ii)转化为c≥f(x)
min,从而求函数f(x)在区间
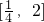
上的最小值,从而求c的值
(II)当a=b时,f(x)=
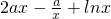
①a=0符合条件
②a≠0时,分a>0,a<0讨论f′(x)在(0,+∞)上的正负,以确定函数的单调性的条件,进而求出a的取值范围
点评:本题(I)(i)考查了函数取得极值的性质:若函数在x
0处取得极值?则f(x
0)=0,但f′(x
0)=0,x
0不一定是函数的极值点,即某点的导数为0是该点为极值的必要不充分条件.
(ii)注意是“存在”
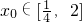
,使得c≥f(x
0)成立?c≥f(x
0)
min;
若是“任意”
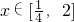
使得c≥f(x)恒成立?c≥f(x)
max,要区别两种不同的情况.
(II)结合极值考查函数的单调性,需要注意分类讨论的思想在解题中的应用.

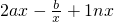
 处取得极值,
处取得极值,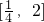 存在x0,使得不等式f(xo)-c≤0成立,求c最小值
存在x0,使得不等式f(xo)-c≤0成立,求c最小值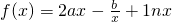 ,∴
,∴ .(1分)
.(1分) 处取得极值,∴
处取得极值,∴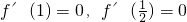 (2分)
(2分)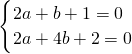 解得
解得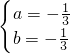
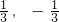 (4分)
(4分)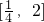 存在xo,使得不等式f(xo)-c≤0成立,只需c≥[f(x)]min,
存在xo,使得不等式f(xo)-c≤0成立,只需c≥[f(x)]min,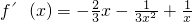 =
=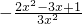 =
= ,
, 时,f'(x)<0,故f(x)在
时,f'(x)<0,故f(x)在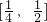 是单调递减;
是单调递减;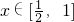 时,f'(x)>0,故f(x)在
时,f'(x)>0,故f(x)在 是单调递增;
是单调递增; 是f(x)在
是f(x)在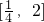 上的极小值.(6分)
上的极小值.(6分)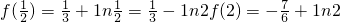 ,
,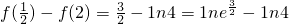 ,
, ,
,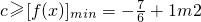 ,∴c的取值范围为
,∴c的取值范围为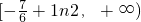 ,
,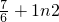 .(9分)
.(9分)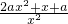 ,
,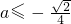 ,此时f(x)在(0+∞)上单调递减;
,此时f(x)在(0+∞)上单调递减; .(14分)
.(14分)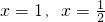 取得极值,则
取得极值,则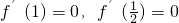 ,代入可求a,b的值.
,代入可求a,b的值.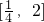 上的最小值,从而求c的值
上的最小值,从而求c的值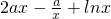
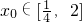 ,使得c≥f(x0)成立?c≥f(x0)min;
,使得c≥f(x0)成立?c≥f(x0)min;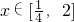 使得c≥f(x)恒成立?c≥f(x)max,要区别两种不同的情况.
使得c≥f(x)恒成立?c≥f(x)max,要区别两种不同的情况.
