
 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.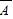 )=
)=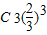 =
=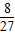 ,
,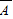 )=
)=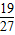 .…(4分)
.…(4分) ,P(X=2)=
,P(X=2)=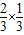 =
= ,P(X=3)=1-
,P(X=3)=1- -
- =
= ,…(8分)
,…(8分)| X | 1 | 2 | 3 |
| P |  |  |  |
 ×1+
×1+ ×2+
×2+ ×3=
×3=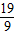 .…(10分)
.…(10分)

科目:高中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源:2013届北京西城(北区)高二下学期学业测试理科数学试卷(解析版) 题型:解答题
甲同学在军训中,练习射击项目,他射击命中目标的概率是 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.
(Ⅰ)在3次射击中,求甲至少有1次命中目标的概率;
(Ⅱ)在射击中,若甲命中目标,则停止射击,否则继续射击,直至命中目标,但射击次数最多不超过3次,求甲射击次数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com