
如下图,已知P为△ABC所在平面外一点,PC⊥AB,PC=AB=2,E、F分别为PA和BC的中点.
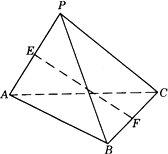
(1)求证:EF与PC是异面直线;
(2)EF与PC所成的角;
(3)线段EF的长.
|
解析:(1)用反证法.假设EF与PC共面于α,则直线PE、CF共面α,则A∈α,B∈α,于是P与A、B、C共面于α,这与已知“P是平面ABC外一点”矛盾.故EF与PC是异面直线. (2)取PB中点G,连结EG、FG,由E、F分别是线段PA、BC中点,有EG (3)由(2)知Rt△EGF中EG=1,GF=1,∠EGF=90°,∴EF= |


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
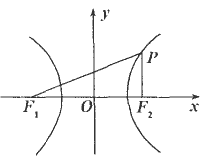
如下图,已知F1、F2为双曲线![]() -
-![]() =1(a>0,b>0)的焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=
=1(a>0,b>0)的焦点,过F2作垂直于x轴的直线交双曲线于点P,且∠PF1F2=![]() .求双曲线的渐近线方程.
.求双曲线的渐近线方程.
查看答案和解析>>
科目:高中数学 来源:重难点手册 高中数学·必修4(配人教A版新课标) 人教A版新课标 题型:022
如下图,已知四边形ABCD是矩形,O为对角线AC与BD的交点,设点集M={O,A,B,C,D},向量的集合T={![]() |P,Q∈M,且P、Q不重合},则集合T有________个子集.
|P,Q∈M,且P、Q不重合},则集合T有________个子集.

查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高一版(必修4) 2009-2010学年 第46期 总202期 北师大课标版 题型:013
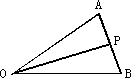
如下图,已知△AOB,点P在线段AB上,且满足![]() =2t
=2t![]() +t
+t![]() (t∈R),设
(t∈R),设![]() =λ
=λ![]() ,则λ的值为
,则λ的值为
![]()
![]()
2
3
查看答案和解析>>
科目:高中数学 来源:导学大课堂必修二数学苏教版 苏教版 题型:044
如下图,已知三棱锥P-ABC中,E、F分别是以AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.

(1)证明PC⊥平面PAB;
(2)求二面角P-AB-C的平面角的余弦值;
(3)若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.
查看答案和解析>>
科目:高中数学 来源: 题型:

①![]() ②
②![]() ③
③![]() ④
④![]() ⑤
⑤![]()
A.1个 B.2个 C.4个 D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com