
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
![]()
表2:女生
![]()
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
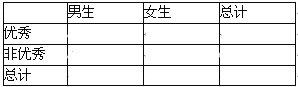
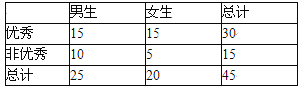
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考数据与公式:
K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
![]()
【答案】(1)![]() ;(2)没有
;(2)没有![]() 的把握认为“测评结果优秀与性别有关”
的把握认为“测评结果优秀与性别有关”
【解析】试题分析:(1)根据分层抽样抽样比相等,求出x,y的值,从表2中非优秀学生共5人,从这5人中任选2人的所有可能结果共10种,其中恰有1人测评等级为合格”的结果共6种,故所求概率为![]() .
.
(2)由1﹣0.9=0.1,p(k2>2.706)=0.10,计算K2=![]() =
=![]() =
=![]() =1.125<2.706,可得没有90%的把握认为“测评结果优秀与性别有关”.
=1.125<2.706,可得没有90%的把握认为“测评结果优秀与性别有关”.
试题解析:(1)设从高一年级男生中抽出m人,则![]() =
=![]() ,m=25,
,m=25,
∴x=25﹣20=5,y=20﹣18=2,
表2中非优秀学生共5人,记测评等级为合格的3人为a,b,c,尚待改进的2人为A,B,
则从这5人中任选2人的所有可能结果为:(a,b)(a,c)(b,c)(A,B)(a,A),(a,B),(b,A)(,b,B),(c,A)(c,B),共10种.
设事件C表示“从表二的非优秀学生5人中随机选取2人,恰有1人测评等级为合格”,
则C的结果为:(a,A),(a,B),(b,A)(,b,B),(c,A)(c,B),共6种.
∴P(C)=![]() =
=![]() ,故所求概率为
,故所求概率为![]() .
.
(2)∵1﹣0.9=0.1,p(k2>2.706)=0.10,
而K2=![]() =
=![]() =
=![]() =1.125<2.706,
=1.125<2.706,
所以没有90%的把握认为“测评结果优秀与性别有关”.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使![]() =
=![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
⑴当![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 内有两个不同的不动点,求实数
内有两个不同的不动点,求实数![]() 的取值范围;
的取值范围;
(3)若对于任意实数![]() ,函数
,函数![]() 恒有两个不相同的不动点,求实数
恒有两个不相同的不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个.求:
(1)连续取两次都是红球的概率;
(2)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数![]() 的概率分布列及期望.
的概率分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2014山东.理15】已知函数![]() ,对函数
,对函数![]() ,定义
,定义![]() 关于
关于![]() 的对称函数为函数
的对称函数为函数![]() ,
,![]() 满足:对于任意
满足:对于任意![]() ,两个点
,两个点![]() 关于点
关于点![]() 对称,若
对称,若![]() 是
是![]() 关于
关于![]() 的“对称函数”,且
的“对称函数”,且![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
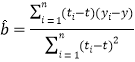 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
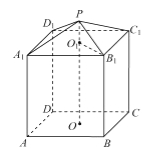
【题目】【2016高考江苏卷】现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥![]() ,下部分的形状是正四棱柱
,下部分的形状是正四棱柱![]() (如图所示),并要求正四棱柱的高
(如图所示),并要求正四棱柱的高![]() 的四倍.
的四倍.
(1)若![]() 则仓库的容积是多少?
则仓库的容积是多少?
(2)若正四棱柱的侧棱长为6m,则当![]() 为多少时,仓库的容积最大?
为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形![]() (及其内部)以
(及其内部)以![]() 边所在直线为旋转轴旋转
边所在直线为旋转轴旋转![]() 得到的,
得到的, ![]() 是
是![]() 的中点.
的中点.
(![]() )设
)设![]() 是
是![]() 上的一点,且
上的一点,且![]() ,求
,求![]() 的大小;
的大小;
(![]() )当
)当![]() 时,求二面角
时,求二面角![]() 的大小.
的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com