
【题目】已知函数![]() .
.
![]() 1
1![]() 若
若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
![]() 2
2![]() 若对任意的
若对任意的![]() ,
,![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 当
当![]() 时,以
时,以![]() 在
在![]() 单调递增,
单调递增,![]() 单调递减;(
单调递减;(![]() 当
当![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,![]() ,
,![]() 单调递减;(2)
单调递减;(2)![]() .
.
【解析】
![]() 1
1![]() 求出
求出![]() ,分两种情况讨论
,分两种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;
的减区间;![]() 2
2![]() 求出
求出![]() 的最大值,问题等价于
的最大值,问题等价于![]() ,即
,即![]() ,对
,对![]() 恒成立,求出函数的导数,通过讨论
恒成立,求出函数的导数,通过讨论![]() 的范围,结合函数的单调性,可筛选出符合题意的
的范围,结合函数的单调性,可筛选出符合题意的![]() 的范围.
的范围.
![]() 1
1![]() 由题意,
由题意,
![]() .
.
![]() 当
当![]() 时,
时,![]() ,令
,令![]() 得
得![]() ;
;![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 单调递增,
单调递增,![]() 单调递减;
单调递减;
(![]() 当
当![]() 时,
时,![]() ,令
,令![]() 得
得![]() ;
;
令![]() ,得
,得![]() 或
或![]() ,所以,
,所以,![]() 在
在![]() 单调递增,
单调递增,![]() ,
,![]() 单调递减.
单调递减.
![]() 2
2![]() 令
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,则
单调递增,则![]() ,
,
则![]() 对
对![]() 恒成立等价于
恒成立等价于![]() ,
,
即![]() ,对
,对![]() 恒成立.
恒成立.
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,此时
,此时![]() ,
,
不合题意,舍去 .
![]() 当
当![]() 时,令
时,令![]() ,
,![]() ,
,
则![]() ,其中
,其中![]() ,
,![]() ,
,
令![]() ,
,![]() ,则
,则![]() 在区间
在区间![]() 上单调递增.
上单调递增.
![]() 当
当![]() 时,
时,![]() ,所以对
,所以对![]() ,
,![]() ,
,
则![]() 在
在![]() 上单调递增,故对任意
上单调递增,故对任意![]() ,
,![]() ,
,
即不等式![]() 在
在![]() 上恒成立,满足题意
上恒成立,满足题意![]()
![]() 当
当![]() 时,由
时,由![]() ,
,![]() 及
及![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以存在唯一的![]() 使得
使得![]() ,且
,且![]() 时,
时,![]() .
.
从而![]() 时,
时,![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() 时,
时,![]() ,即
,即![]() ,不符合题意.
,不符合题意.
综上所述,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某超市2018年12个月的收入与支出数据的折线图如图所示:

根据该折线图可知,下列说法错误的是( )
A. 该超市2018年的12个月中的7月份的收益最高
B. 该超市2018年的12个月中的4月份的收益最低
C. 该超市2018年1-6月份的总收益低于2018年7-12月份的总收益
D. 该超市2018年7-12月份的总收益比2018年1-6月份的总收益增长了90万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,在四棱锥![]() 中,
中,![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
(1)求证:![]() 面
面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,满足
,满足![]() ?若存在,试求出二面角
?若存在,试求出二面角![]() 的余弦值;若不存在,说明理由。
的余弦值;若不存在,说明理由。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
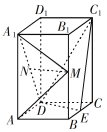
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com