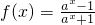练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数数学公式（a＞0且a≠1）．
    （1）判断f（x）的奇偶性；
    （2）当a＞1时，判断f（x）在（-∞，+∞）上的单调性，并加以证明．

    （1）解：由f（x）的定义域为（-∞，+∞），关于数0对称（2分），得∴f（x）为R上的奇函数．（6分）
    （2）当a＞1时，f（x）在（-∞，+∞）上的单调递增．（8分）（本次未扣分，以后考试一定会扣分）
    证明：设x1，x2为（-∞，+∞）上任意两个实数，且x1＜x2，
    则由a＞1得

    ∴当a＞1时，f（x）在（-∞，+∞）上的单调递增．（14分）
    分析：（1）用奇偶性定义判断，先看f（x）的定义域是否关于原点对称，再看f（x）与f（-x）的关系．
    （2）用单调性定义判断，思路是在区间上任取两个变量，且界定大小，再作差变形看符号．
    点评：本题主要考查函数的奇偶性和单调性的判断．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若函数y=f（x），x∈D同时满足下列条件：
    （1）在D内的单调函数；
    （2）存在实数m，n，当定义域为[m，n]时，值域为[m，n]．则称此函数为D内可等射函数，设f(x)=
    ax+a-3lna
    （a＞0且a≠1），则当f （x）为可等射函数时，a的取值范围是
    （0，1）∪（1，2）
    （0，1）∪（1，2）
    ．

    查看答案和解析>>

    科目：高中数学 来源：福建省安溪一中、惠安一中、养正中学2011－2012学年高一上学期期中联考数学试题 题型：044

    若函数f(x)满足下列条件：在定义域内存在x0，使得f(x0＋1)＝f(x0)＋f(1)成立，则称函数f(x)具有性质M；反之，若x0不存在，则称函数f(x)不具有性质M．

    (Ⅰ)证明：函数f(x)＝2x具有性质M，并求出对应的x0的值；

    (Ⅱ)已知函数h(x)＝lg具有性质M，求a的取值范围；

    (Ⅲ)试探究形如①y＝kx＋b(k≠0)、②y＝ax2＋bx＋c(a≠0)、③y＝(k≠0)、④y＝ax(a＞0且a≠1)、⑤y＝logax(a＞0且a≠1)的函数，指出哪些函数一定具有性质M？并加以证明．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若函数y=f（x），x∈D同时满足下列条件：
    （1）在D内的单调函数；
    （2）存在实数m，n，当定义域为[m，n]时，值域为[m，n]．则称此函数为D内可等射函数，设f(x)=
    ax+a-3
    lna
    （a＞0且a≠1），则当f （x）为可等射函数时，a的取值范围是______．

    查看答案和解析>>

    科目：高中数学 来源：2012年四川省绵阳市培城区南山中学高考数学三模试卷（文科）（解析版） 题型：解答题

    若函数f（x）具有性质：，则称f（x）是满足“倒负”变换的函数．下列四个函数：
    ①f（x）=logax（a＞0且a≠1）；        
    ②f（x）=ax（a＞0且a≠1）；
    ③；                      
     ④．
    其中，满足“倒负”变换的所有函数的序号是    ．

    查看答案和解析>>

    同步练习册答案