
【题目】已知曲线![]() ,
,![]() 为曲线
为曲线![]() 上一动点,过
上一动点,过![]() 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是![]() 和
和![]() .
.
(1)当![]() 运动到
运动到![]() 时,求
时,求![]() 的值;
的值;
(2)设直线![]() (不与
(不与![]() 轴垂直)与曲线
轴垂直)与曲线![]() 交于
交于![]() 、
、![]() 两点,与
两点,与![]() 轴正半轴交于
轴正半轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点,若
点,若![]() ,
,![]() ,且
,且![]() ,求证
,求证![]() 为定点.
为定点.
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),将
),将![]() 的图象上所有点的横坐标缩短到原来的
的图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),再将得到的图象上所有点向右平行移动
倍(纵坐标不变),再将得到的图象上所有点向右平行移动![]() 个单位长度,得到
个单位长度,得到![]() 的图象,则以下关于函数
的图象,则以下关于函数![]() 的结论正确的是( )
的结论正确的是( )
A.若![]() ,
,![]() 是
是![]() 的零点,则
的零点,则![]() 是
是![]() 的整数倍
的整数倍
B.函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C.点![]() 是函数
是函数![]() 图象的对称中心
图象的对称中心
D.![]() 是函数
是函数![]() 图象的对称轴
图象的对称轴
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数(comsummer priceindex)的简称.居民消费价格指数是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.如图是根据国家统计局发布的2019年4月——2020年4月我国CPI涨跌幅数据绘制的折线图(注:2019年6月与2018年6月相比较,叫同比;2019年6月与2019年5月相比较,叫环比),根据该折线图,则下列结论正确的是( )
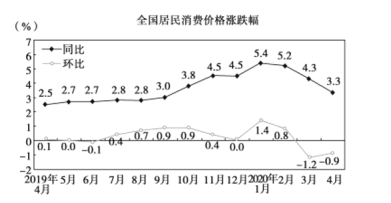
A.2019年4月至2020年4月各月与去年同期比较,CPI有涨有跌
B.2019年4月居民消费价格同比涨幅最小,2020年1月同比涨幅最大
C.2020年1月至2020年4月CPI只跌不涨
D.2019年4月至2019年6月CPI涨跌波动不大,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车已经走进我们的生活,逐渐为大家所青睐.现在有某品牌的新能源汽车在甲市进行预售,预售场面异常火爆,故该经销商采用竞价策略基本规则是:①竞价者都是网络报价,每个人并不知晓其他人的报价,也不知道参与竞价的总人数;②竞价采用“一月一期制”,当月竞价时间截止后,系统根据当期汽车配额,按照竞价人的出价从高到低分配名额.某人拟参加2020年6月份的汽车竞价,他为了预测最低成交价,根据网站的公告,统计了最近5个月参与竞价的人数(如下表)
月份 | 2020.01 | 2020.02 | 2020.03 | 2020.04 | 2020.05 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
竞拍人数 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)由收集数据的散点图发现,可用线性回归模型拟合竞价人数y(万人)与月份编号t之间的相关关系.请用最小二乘法求y关于t的线性回归方程:![]() ,并预测2020年6月份(月份编号为6)参与竞价的人数;
,并预测2020年6月份(月份编号为6)参与竞价的人数;
(2)某市场调研机构对200位拟参加2020年6月份汽车竞价人员的报价进行了一个抽样调查,得到如表所示的频数表:
报价区间(万元) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位竞价人员报价的平均值![]() 和样本方差s2(同一区间的报价用该价格区间的中点值代替)
和样本方差s2(同一区间的报价用该价格区间的中点值代替)
(ii)假设所有参与竞价人员的报价X可视为服从正态分布![]() 且μ与σ2可分别由(i)中所示的样本平均数
且μ与σ2可分别由(i)中所示的样本平均数![]() 及s2估计.若2020年月6份计划提供的新能源车辆数为3174,根据市场调研,最低成交价高于样本平均数
及s2估计.若2020年月6份计划提供的新能源车辆数为3174,根据市场调研,最低成交价高于样本平均数![]() ,请你预测(需说明理由)最低成交价.
,请你预测(需说明理由)最低成交价.
参考公式及数据:
①回归方程![]() ,其中
,其中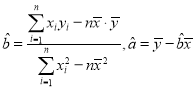
②![]()
③若随机变量X服从正态分布![]() 则
则![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人.某单位有老年员工
日,我国开始施行《个人所得税专项附加扣除操作办法》,附加扣除的专项包括子女教育、继续教育、大病医疗、住房贷款利息、住房租金、赡养老人.某单位有老年员工![]() 人,中年员工
人,中年员工![]() 人,青年员工
人,青年员工![]() 人,现采用分层抽样的方法,从该单位员工中抽取
人,现采用分层抽样的方法,从该单位员工中抽取![]() 人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如表:
人,调查享受个人所得税专项附加扣除的情况,并按照员工类别进行各专项人数汇总,数据统计如表:
专项员工人数 | 子女教育 | 继续教育 | 大病医疗 | 住房贷款利息 | 住房租金 | 赡养老人 |
老员工 |
|
|
|
|
|
|
中年员工 |
|
|
|
|
|
|
青年员工 |
|
|
|
|
|
|
(Ⅰ)在抽取的![]() 人中,老年员工、中年员工、青年员工各有多少人;
人中,老年员工、中年员工、青年员工各有多少人;
(Ⅱ)从上表享受住房贷款利息专项扣除的员工中随机选取![]() 人,记
人,记![]() 为选出的中年员工的人数,求
为选出的中年员工的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 底面
底面![]() ,点
,点![]() 是棱
是棱![]() 的中点,平面
的中点,平面![]() 与棱
与棱![]() 相交于点
相交于点![]() .
.
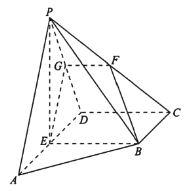
(1)求证:![]() ;
;
(2)若![]() 与
与![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com