
【题目】已知函数f(x)=2x-![]() .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
【答案】(1) x=log2(1+![]() ) (2) [-5,+∞)
) (2) [-5,+∞)
【解析】
试题分析:(1)化简f(x)=0,然后,针对x进行讨论;(2)由2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,得![]() 对于t∈[1,2]恒成立,整理后分离参数m,利用配方法求出含有变量t的函数的最大值得答案
对于t∈[1,2]恒成立,整理后分离参数m,利用配方法求出含有变量t的函数的最大值得答案
试题解析:(1)当x<0时,f(x)=0;当x≥0时,f(x)=2x-![]() . ...........3分
. ...........3分
由条件可知2x-![]() =2,即22x-2·2x-1=0,
=2,即22x-2·2x-1=0,
解得2x=1±![]() . ....................5分
. ....................5分
∵2x>0,∴x=log2(1+![]() ). ....................6分
). ....................6分
(2)当t∈[1,2]时,2t![]() +m
+m![]() ≥0, ..........7分
≥0, ..........7分
即m(22t-1)≥-(24t-1).
∵22t-1>0,∴m≥-(22t+1).∵t∈[1,2],................9分
∴-(1+22t)∈[-17,-5],.....................10分
故m的取值范围是[-5,+∞).................12分


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,某小区准备将一块闲置的直角三角形(其中![]() )土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道
)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道![]() ,且两边是两个关于走道
,且两边是两个关于走道![]() 对称的三角形(
对称的三角形(![]() 和
和![]() ),现考虑方便和绿地最大化原则,要求
),现考虑方便和绿地最大化原则,要求![]() 点与
点与![]() 点不重合,
点不重合,![]() 点落在边
点落在边![]() 上,设
上,设![]() .
.
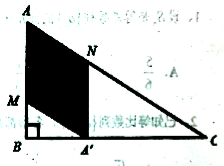
(1)若![]() ,绿地“最美”,求最美绿地的面积;
,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民行走,设计时要求![]() 最短,求此时公共绿地走道
最短,求此时公共绿地走道![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,离心率
,离心率![]() ,过点
,过点![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,且与
,且与![]() 轴不重合,交椭圆
轴不重合,交椭圆![]() 于
于![]() 两点,过点
两点,过点![]() 且与
且与![]() 垂直的直线与圆
垂直的直线与圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在如下图象中的两条线段上.该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:
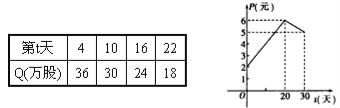
(1)根据提供的图象,写出该种股票每股的交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几天日交易额最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.

(1)求证:BC∥DE;
(2)若D、E、C、F四点共圆,且![]() ,求∠BAC.
,求∠BAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点![]() 为中心的
为中心的![]() 海里以内海域被设为警戒水域.点
海里以内海域被设为警戒水域.点![]() 正北
正北![]() 海里有一个雷达观测站
海里有一个雷达观测站![]() ,某时刻测得一艘匀速直线行驶的船只位于点
,某时刻测得一艘匀速直线行驶的船只位于点![]() 北偏东
北偏东![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() ,经过
,经过![]() 分钟又测得该船已行驶到点
分钟又测得该船已行驶到点![]() 北偏东
北偏东![]() (其中
(其中![]() 且与点
且与点![]() 相距
相距![]() 海里的位置
海里的位置![]() .
.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com