
ΓΨΧβΡΩΓΩ÷Ϋ’≈ΒΡΙφΗώ «÷Η÷Ϋ’≈÷Τ≥…ΚσΘ§Ψ≠Ιΐ–ό’ϊ«–±ΏΘ§≤Ο≥…“ΜΕ®ΒΡ≥Ώ¥γ.œ÷‘ΎΈ“Ιζ≤…”ΟΙζΦ ±ξΉΦΘ§ΙφΕ®“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Β»±ξΦ«ά¥±μ Ψ÷Ϋ’≈ΒΡΖυΟφΙφΗώ.Η¥”Γ÷ΫΖυΟφΙφΗώ÷Μ≤…”Ο
Β»±ξΦ«ά¥±μ Ψ÷Ϋ’≈ΒΡΖυΟφΙφΗώ.Η¥”Γ÷ΫΖυΟφΙφΗώ÷Μ≤…”Ο![]() œΒΝ–ΚΆ
œΒΝ–ΚΆ![]() œΒΝ–Θ§Τδ÷–œΒΝ–ΒΡΖυΟφΙφΗώΈΣΘΚΔΌ
œΒΝ–Θ§Τδ÷–œΒΝ–ΒΡΖυΟφΙφΗώΈΣΘΚΔΌ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Υυ”–ΙφΗώΒΡ÷Ϋ’≈ΒΡΖυΩμΘ®“‘
Υυ”–ΙφΗώΒΡ÷Ϋ’≈ΒΡΖυΩμΘ®“‘![]() ±μ ΨΘ©ΚΆ≥ΛΕ»Θ®“‘
±μ ΨΘ©ΚΆ≥ΛΕ»Θ®“‘![]() ±μ ΨΘ©ΒΡ±»άΐΙΊœΒΕΦΈΣ
±μ ΨΘ©ΒΡ±»άΐΙΊœΒΕΦΈΣ![]() ΘΜΔΎΫΪ
ΘΜΔΎΫΪ![]() ÷Ϋ’≈―Ί≥ΛΕ»ΖΫœρΕ‘ΩΣ≥…ΝΫΒ»Ζ÷Θ§±ψ≥…ΈΣ
÷Ϋ’≈―Ί≥ΛΕ»ΖΫœρΕ‘ΩΣ≥…ΝΫΒ»Ζ÷Θ§±ψ≥…ΈΣ![]() ΙφΗώΘ§
ΙφΗώΘ§![]() ÷Ϋ’≈―Ί≥ΛΕ»ΖΫœρΕ‘ΩΣ≥…ΝΫΒ»Ζ÷Θ§±ψ≥…ΈΣ
÷Ϋ’≈―Ί≥ΛΕ»ΖΫœρΕ‘ΩΣ≥…ΝΫΒ»Ζ÷Θ§±ψ≥…ΈΣ![]() ΙφΗώΘ§Γ≠Θ§»γ¥ΥΕ‘ΩΣ÷Ν
ΙφΗώΘ§Γ≠Θ§»γ¥ΥΕ‘ΩΣ÷Ν![]() ΙφΗώ.œ÷”–
ΙφΗώ.œ÷”–![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷ΫΗς“Μ’≈.»τ
÷ΫΗς“Μ’≈.»τ![]() ÷ΫΒΡΩμΕ»ΈΣ
÷ΫΒΡΩμΕ»ΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ÷ΫΒΡΟφΜΐΈΣ________
÷ΫΒΡΟφΜΐΈΣ________![]() ΘΜ’β
ΘΜ’β![]() ’≈÷ΫΒΡΟφΜΐ÷°ΚΆΒ»”Ύ________
’≈÷ΫΒΡΟφΜΐ÷°ΚΆΒ»”Ύ________![]() .
.
ΓΨ¥πΑΗΓΩ![]()
![]()
ΓΨΫβΈωΓΩ
Ω……η![]() ΒΡ÷Ϋ’≈ΒΡ≥ΛΕ»ΈΣ
ΒΡ÷Ϋ’≈ΒΡ≥ΛΕ»ΈΣ![]() Θ§‘ρ ΐΝ–
Θ§‘ρ ΐΝ–![]() ≥…“‘
≥…“‘![]() ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§…η
ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§…η![]() ΒΡ÷Ϋ’≈ΒΡΟφΜΐ
ΒΡ÷Ϋ’≈ΒΡΟφΜΐ![]() Θ§‘ρ ΐΝ–
Θ§‘ρ ΐΝ–![]() ≥…“‘
≥…“‘![]() ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§»ΜΚσάϊ”ΟΒ»±» ΐΝ–ΒΡΆ®œνΙΪ Ϋ«σ≥ω ΐΝ–
ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§»ΜΚσάϊ”ΟΒ»±» ΐΝ–ΒΡΆ®œνΙΪ Ϋ«σ≥ω ΐΝ–![]() ΒΡ ΉœνΘ§≤Δάϊ”ΟΒ»±» ΐΝ–ΒΡ«σΚΆΙΪ Ϋ«σ≥ω
ΒΡ ΉœνΘ§≤Δάϊ”ΟΒ»±» ΐΝ–ΒΡ«σΚΆΙΪ Ϋ«σ≥ω![]() ΒΡ«Α
ΒΡ«Α![]() œν÷°ΚΆ.
œν÷°ΚΆ.
Ω……η![]() ΒΡ÷Ϋ’≈ΒΡ≥ΛΕ»ΈΣ
ΒΡ÷Ϋ’≈ΒΡ≥ΛΕ»ΈΣ![]() Θ§ΟφΜΐΈΣ
Θ§ΟφΜΐΈΣ![]() Θ§
Θ§![]() ΒΡΩμΕ»ΈΣ
ΒΡΩμΕ»ΈΣ![]() Θ§
Θ§
![]() ΒΡ≥ΛΕ»ΈΣ
ΒΡ≥ΛΕ»ΈΣ![]() Θ§Υυ“‘Θ§ ΐΝ–
Θ§Υυ“‘Θ§ ΐΝ–![]() «“‘
«“‘![]() ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§
ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§
”…Χβ“β÷Σ![]() ÷ΫΒΡΩμΕ»ΈΣ
÷ΫΒΡΩμΕ»ΈΣ![]() Θ§
Θ§![]() Θ§
Θ§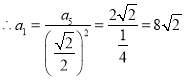 Θ§
Θ§
Υυ“‘Θ§![]() ÷ΫΒΡΟφΜΐΈΣ
÷ΫΒΡΟφΜΐΈΣ![]() Θ§
Θ§
”÷![]() Θ§
Θ§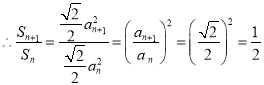 Θ§
Θ§
Υυ“‘Θ§ ΐΝ–![]() «“‘
«“‘![]() ΈΣ ΉœνΘ§“‘
ΈΣ ΉœνΘ§“‘![]() ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§
ΈΣΙΪ±»ΒΡΒ»±» ΐΝ–Θ§
“ρ¥ΥΘ§’β![]() ’≈÷ΫΒΡΟφΜΐ÷°ΚΆΒ»”Ύ
’≈÷ΫΒΡΟφΜΐ÷°ΚΆΒ»”Ύ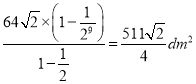 .
.
Ι ¥πΑΗΈΣΘΚ![]() ΘΜ
ΘΜ![]() .
.


 ΟœΫ®ΤΫΟϊ–ΘΩΦΨμœΒΝ–¥πΑΗ
ΟœΫ®ΤΫΟϊ–ΘΩΦΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() ΒΡΫΙΒψΈΣFΘ§AΈΣC…œ“λ”Ύ‘≠ΒψΒΡ»Έ“β“ΜΒψΘ§ΙΐΒψAΒΡ÷±œΏΫΜy÷α’ΐΑκ÷α”ΎΒψBΘ§«“”–
ΒΡΫΙΒψΈΣFΘ§AΈΣC…œ“λ”Ύ‘≠ΒψΒΡ»Έ“β“ΜΒψΘ§ΙΐΒψAΒΡ÷±œΏΫΜy÷α’ΐΑκ÷α”ΎΒψBΘ§«“”–![]() Θ§Β±ΒψAΒΡΉίΉχ±ξΈΣ6 ±Θ§
Θ§Β±ΒψAΒΡΉίΉχ±ξΈΣ6 ±Θ§![]() ΈΣ’ΐ»ΐΫ«–Έ.
ΈΣ’ΐ»ΐΫ«–Έ.
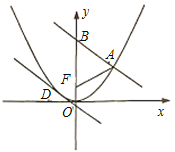
Θ®1Θ©«σCΒΡΖΫ≥ΧΘΜ
Θ®2Θ©»τ÷±œΏ![]() Θ§«“
Θ§«“![]() ΚΆC”–«“÷Μ”–“ΜΗωΙΪΙ≤ΒψDΘ§÷ΛΟςΘΚ÷±œΏADΙΐΕ®ΒψΘ§≤Δ«σ≥ωΗΟΕ®ΒψΉχ±ξ.
ΚΆC”–«“÷Μ”–“ΜΗωΙΪΙ≤ΒψDΘ§÷ΛΟςΘΚ÷±œΏADΙΐΕ®ΒψΘ§≤Δ«σ≥ωΗΟΕ®ΒψΉχ±ξ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§![]() «’ΐΖΫ–ΈΘ§Βψ
«’ΐΖΫ–ΈΘ§Βψ![]() ‘Ύ“‘
‘Ύ“‘![]() ΈΣ÷±ΨΕΒΡΑκ‘≤ΜΓ…œΘ®
ΈΣ÷±ΨΕΒΡΑκ‘≤ΜΓ…œΘ®![]() ≤Μ”κ
≤Μ”κ![]() Θ§
Θ§![]() ÷ΊΚœΘ©Θ§
÷ΊΚœΘ©Θ§![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ΒΡ÷–ΒψΘ§œ÷ΫΪ’ΐΖΫ–Έ
ΒΡ÷–ΒψΘ§œ÷ΫΪ’ΐΖΫ–Έ![]() ―Ί
―Ί![]() ’έΤπΘ§ ΙΒΟΤΫΟφ
’έΤπΘ§ ΙΒΟΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() .
.

Θ®1Θ©÷ΛΟςΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() .
.
Θ®2Θ©»τ![]() Θ§Β±»ΐάβΉΕ
Θ§Β±»ΐάβΉΕ![]() ΒΡΧεΜΐΉν¥σ ±Θ§«σ
ΒΡΧεΜΐΉν¥σ ±Θ§«σ![]() ΒΫΤΫΟφ
ΒΫΤΫΟφ![]() ΒΡΨύάκ.
ΒΡΨύάκ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ°
Θ°
Θ®1Θ©«σΚ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒΡΒΞΒς«χΦδΘΜ
…œΒΡΒΞΒς«χΦδΘΜ
Θ®2Θ©”Ο![]() ±μ Ψ
±μ Ψ![]() ÷–ΒΡΉν¥σ÷ΒΘ§
÷–ΒΡΉν¥σ÷ΒΘ§![]() ΈΣ
ΈΣ![]() ΒΡΒΦΚ· ΐΘ§…ηΚ· ΐ
ΒΡΒΦΚ· ΐΘ§…ηΚ· ΐ![]() Θ§»τ
Θ§»τ![]() ‘Ύ
‘Ύ![]() …œΚψ≥…ΝΔΘ§«σ Β ΐ
…œΚψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©÷ΛΟςΘΚ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ÷±œΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ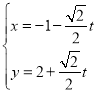 Θ®Τδ÷–
Θ®Τδ÷–![]() ΈΣ≤Έ ΐΘ©Θ§“‘‘≠ΒψΈΣΦΪΒψΘ§“‘
ΈΣ≤Έ ΐΘ©Θ§“‘‘≠ΒψΈΣΦΪΒψΘ§“‘![]() ÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏ
÷αΈΣΦΪ÷αΫ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≥Θ ΐΘ§«“
ΈΣ≥Θ ΐΘ§«“![]() Θ©Θ§÷±œΏ
Θ©Θ§÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψ.
ΝΫΒψ.
Θ®1Θ©»τ![]() Θ§«σ Β ΐ
Θ§«σ Β ΐ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©»τΒψ![]() ΒΡ÷±Ϋ«Ήχ±ξΈΣ
ΒΡ÷±Ϋ«Ήχ±ξΈΣ![]() Θ§«“
Θ§«“![]() Θ§«σ Β ΐ
Θ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηOΈΣΉχ±ξ‘≠ΒψΘ§Ε·ΒψM‘ΎΆ÷‘≤C![]() …œΘ§ΙΐMΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣNΘ§ΒψP¬ζΉψ
…œΘ§ΙΐMΉςx÷αΒΡ¥ΙœΏΘ§¥ΙΉψΈΣNΘ§ΒψP¬ζΉψ![]() .
.
Θ®1Θ©«σΒψPΒΡΙλΦΘΖΫ≥ΧΘΜ
Θ®2Θ©…ηΒψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ§«“
…œΘ§«“![]() .÷ΛΟςΘΚΙΐΒψP«“¥Ι÷±”ΎOQΒΡ÷±œΏ
.÷ΛΟςΘΚΙΐΒψP«“¥Ι÷±”ΎOQΒΡ÷±œΏ![]() ΙΐCΒΡΉσΫΙΒψF.
ΙΐCΒΡΉσΫΙΒψF.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΒςΫΎΗΏ»ΐ―ß…ζ―ßœΑ―ΙΝΠΘ§Ρ≥–ΘΗΏ»ΐΡξΦΕΨΌ––ΝΥΑΈΚ”±»»ϋΘ§‘Ύ»ϋ«Α»ΐΈΜάœ ΠΕ‘«Α»ΐΟϊΫχ––ΝΥ‘Λ≤βΘ§”Ύ «”–ΝΥ“‘œ¬Ε‘ΜΑΘΚάœ ΠΦΉΘΚΓΑ7ΑύΡ–…ζ±»ΫœΉ≥Θ§7ΑύΩœΕ®ΒΟΒΎ“ΜΟϊΓ±Θ°άœ Π““ΘΚΓΑΈ“ΨθΒΟ14Αύ±»15Αύ«ΩΘ§14ΑύΟϊ¥ΈΜα±»15ΑύΩΩ«ΑΓ±Θ°άœ Π±ϊΘΚΓΑΈ“ΨθΒΟ7ΑύΡή”°15ΑύΓ±Θ°ΉνΚσάœ ΠΕΓ»ΞΙέΩ¥ΆξΝΥ±»»ϋΘ§ΜΊά¥ΚσΥΒΘΚΓΑ»Ζ Β «’β»ΐΗωΑύΒΟΝΥ«Α»ΐΟϊΘ§«“Έό≤ΔΝ–Θ§ΒΪ «ΡψΟ«»ΐ»Υ÷–÷Μ”–“Μ»Υ‘Λ≤βΉΦ»ΖΓ±Θ°Ρ«Ο¥Θ§ΜώΒΟ“ΜΓΔΕΰΓΔ»ΐΟϊΒΡΑύΦΕ“ά¥ΈΈΣ( )
A.7ΑύΓΔ14ΑύΓΔ15ΑύB.14ΑύΓΔ7ΑύΓΔ15Αύ
C.14ΑύΓΔ15ΑύΓΔ7ΑύD.15ΑύΓΔ14ΑύΓΔ7Αύ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»ΐάβ÷υABC©¹A1B1C1÷–Θ§ΤΫΟφAA1B1BΓΆΤΫΟφABCΘ§ABΘΫAA1ΘΫA1BΘΫ4Θ§BCΘΫ2Θ§ACΘΫ2![]() Θ§ΒψFΈΣABΒΡ÷–ΒψΘ§ΒψEΈΣœΏΕΈA1C1…œΒΡΕ·Βψ.
Θ§ΒψFΈΣABΒΡ÷–ΒψΘ§ΒψEΈΣœΏΕΈA1C1…œΒΡΕ·Βψ.
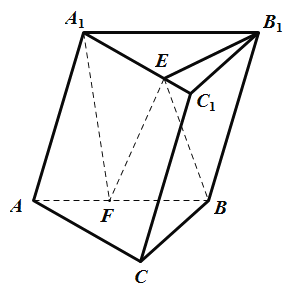
Θ®1Θ©«σ÷ΛΘΚBCΓΆΤΫΟφA1EFΘΜ
Θ®2Θ©»τΓœB1EC1ΘΫ60ΓψΘ§«σΥΡΟφΧεA1B1EFΒΡΧεΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐfΘ®xΘ©ΘΫex©¹ax+aΘ®aΓ RΘ©Θ§ΤδΆΦœσ”κx÷αΫΜ”ΎAΘ®x1Θ§0Θ©Θ§BΘ®x2Θ§0Θ©ΝΫΒψΘ§«“x1ΘΦx2Θ°
Θ®1Θ©«σaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©÷ΛΟςΘΚfΓδΘ®![]() Θ©ΘΦ0Θ®fΓδΘ®xΘ©ΈΣΚ· ΐfΘ®xΘ©ΒΡΒΦΚ· ΐΘ©ΘΜ
Θ©ΘΦ0Θ®fΓδΘ®xΘ©ΈΣΚ· ΐfΘ®xΘ©ΒΡΒΦΚ· ΐΘ©ΘΜ
Θ®3Θ©…ηΒψC‘ΎΚ· ΐyΘΫfΘ®xΘ©ΒΡΆΦœσ…œΘ§«“ΓςABCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Φ«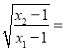 tΘ§«σΘ®a©¹1Θ©Θ®t©¹1Θ©ΒΡ÷ΒΘ°
tΘ§«σΘ®a©¹1Θ©Θ®t©¹1Θ©ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com