
【题目】已知向量![]() ,
,![]() ,角
,角![]() ,
,![]() ,
,![]() 为
为![]() 的内角,其所对的边分别为
的内角,其所对的边分别为![]() ,
,![]() ,
,![]() .
.
(1)当![]() 取得最大值时,求角
取得最大值时,求角![]() 的大小;
的大小;
(2)在(1)成立的条件下,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)由两向量的坐标,利用平面向量的数量积运算列出关系式,利用诱导公式及二倍角的余弦函数公式化简,整理后得到关于![]() 的二次函数,由
的二次函数,由![]() 的范围求出
的范围求出![]() 的范围,利用正弦函数的图象与性质得出此时
的范围,利用正弦函数的图象与性质得出此时![]() 的范围,利用二次函数的性质即可求出
的范围,利用二次函数的性质即可求出![]() 取得最大值时
取得最大值时![]() 的度数;
的度数;
(2)由![]() 及
及![]() 的值,利用正弦定理表示出
的值,利用正弦定理表示出![]() ,再利用三角形的内角和定理用
,再利用三角形的内角和定理用![]() 表示出
表示出![]() ,将表示出的
,将表示出的![]() 代入
代入![]() 中,利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,由
中,利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,由![]() 的范围求出这个角的范围,利用正弦函数的图象与性质求出此时正弦函数的值域,即可确定出
的范围求出这个角的范围,利用正弦函数的图象与性质求出此时正弦函数的值域,即可确定出![]() 的取值范围.
的取值范围.
详解:
(1)![]()
![]() ,令
,令![]() ,
,![]() ,
,
原式![]() ,当
,当![]() ,即
,即![]() ,
,![]() 时,
时,![]() 取得最大值.
取得最大值.
(2)当![]() 时,
时,![]() ,
,![]() .由正弦定理得:
.由正弦定理得:![]() (
(![]() 为
为![]() 的外接圆半径)
的外接圆半径)
于是![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
由![]() ,得
,得![]() ,于是
,于是
![]() ,
,![]() ,
,
所以![]() 的范围是
的范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向形外作正方形
为一边向形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
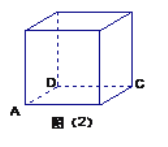
【题目】如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题。
(1)求证:MN∥平面PBD;
(2)求证:![]() 平面
平面![]() ;
;
(3)求PB和平面NMB所成的角的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(2,4),直线l:x﹣2y+1=0.
(1)求过点A且平行于l的直线的方程;
(2)若点M在直线l上,且AM⊥l,求点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应十九大报告提出的实施乡村振兴战略,某村庄投资![]() 万元建起了一座绿色农产品加工厂.经营中,第一年支出
万元建起了一座绿色农产品加工厂.经营中,第一年支出![]() 万元,以后每年的支出比上一年增加了
万元,以后每年的支出比上一年增加了![]() 万元,从第一年起每年农场品销售收入为
万元,从第一年起每年农场品销售收入为![]() 万元(前
万元(前![]() 年的纯利润综合=前
年的纯利润综合=前![]() 年的 总收入-前
年的 总收入-前![]() 年的总支出-投资额
年的总支出-投资额![]() 万元).
万元).
(1)该厂从第几年开始盈利?
(2)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
【答案】(1) 从第![]() 开始盈利(2) 该厂第
开始盈利(2) 该厂第![]() 年年平均纯利润达到最大,年平均纯利润最大值为
年年平均纯利润达到最大,年平均纯利润最大值为![]() 万元
万元
【解析】试题分析:(1)根据公式得到![]() ,令函数值大于0解得参数范围;(2)根据公式得到
,令函数值大于0解得参数范围;(2)根据公式得到![]() ,由均值不等式得到函数最值.
,由均值不等式得到函数最值.
解析:
由题意可知前![]() 年的纯利润总和
年的纯利润总和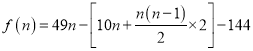
![]()
(1)由![]() ,即
,即![]() ,解得
,解得![]()
由![]() 知,从第
知,从第![]() 开始盈利.
开始盈利.
(2)年平均纯利润![]()
因为![]() ,即
,即![]()
所以![]()
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
年平均纯利润最大值为![]() 万元,
万元,
故该厂第![]() 年年平均纯利润达到最大,年平均纯利润最大值为
年年平均纯利润达到最大,年平均纯利润最大值为![]() 万元.
万元.
【题型】解答题
【结束】
21
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,并且满足
,并且满足![]() ,
, ![]() .
.
(1)求数列![]() 通项公式;
通项公式;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有4个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从盒子中不放回随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从盒子中随机取一个球,该球的编号为![]() ,将球放回盒子中,然后再从盒子中随机取一个球,该球的编号为
,将球放回盒子中,然后再从盒子中随机取一个球,该球的编号为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列{ ![]() }与{
}与{ ![]() },记A={
},记A={ ![]() |
| ![]() =
= ![]() ,
, ![]() },B={
},B={ ![]() |
| ![]() =
= ![]() ,
, ![]() },若同时满足条件:①{
},若同时满足条件:①{ ![]() },{
},{ ![]() }均单调递增;②
}均单调递增;② ![]() 且
且 ![]() ,则称{
,则称{ ![]() }与{
}与{ ![]() }是无穷互补数列.
}是无穷互补数列.
(1)若 ![]() =
= ![]() ,
, ![]() =
= ![]() ,判断{
,判断{ ![]() }与{
}与{ ![]() }是否为无穷互补数列,并说明理由;
}是否为无穷互补数列,并说明理由;
(2)若 ![]() =
= ![]() 且{
且{ ![]() }与{
}与{ ![]() }是无穷互补数列,求数列{
}是无穷互补数列,求数列{ ![]() }的前16项的和;
}的前16项的和;
(3)若{ ![]() }与{
}与{ ![]() }是无穷互补数列,{
}是无穷互补数列,{ ![]() }为等差数列且
}为等差数列且 ![]() =36,求{
=36,求{ ![]() }与{
}与{ ![]() }得通项公式.
}得通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①命题“x0∈R,x02+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量 ![]() 与
与 ![]() 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ ![]()
![]() <0”.
<0”.
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com