已知数列{an}的首项为a1=5,前n项和为Sn,且Sn+1=2Sn+n+5(n∈N*).
(1)证明数列{an+1}是等比数列;
(2)令f(x)=a1x+a2x2+…+anxn,f′(x)是函数f(x)的导函数,令bn=f′(1).求数列{bn}的通项公式.
【答案】
分析:(1)利用递推式,再写一式,两式相减,利用等比数列的定义,即可得到结论;
(2)先确定数列{a
n}的通项,再求导,赋值,再用错位相减法,即可求得数列{b
n}的通项公式.
解答:(1)证明:∵S
n+1=2S
n+n+5,
∴n≥2时,S
n=2S
n-1+n+4,
两式相减可得a
n+1+1=2(a
n+1)
当n=1时,a
2=2a
1+1=11,∴a
2+1=12,
∵a
1=5,∴a
1+1=6,
∴数列{a
n+1}是以6为首项,2为公比的等比数列;
(2)由(1)知a
n+1=6×2
n-1,∴a
n=3×2
n-1,
∵f(x)=a
1x+a
2x
2+…+a
nx
n,
∴f′(x)=a
1+2a
2x+…+na
nx
n-1,
∴f′(1)=a
1+2a
2+…+na
n=(3×2-1)+2(3×2
2-1)+…+n(3×2
n-1)
=3(2+2×2
2+…+n×2
n)-(1+2+3+…+n)
令S=2+2×2
2+…+n×2
n,则2S=2
2+2×2
3+…+n×2
n+1两式相减可得S=(n-1)×2
n+1+2
∴b
n=f′(1)=
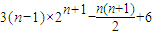
.
点评:本题考查等比数列的证明,考查数列的通项与求和,确定数列的通项,正确运用求和方法是关键.

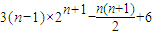 .
.
