
【题目】如图,已知![]() 平面
平面![]()
![]()
![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
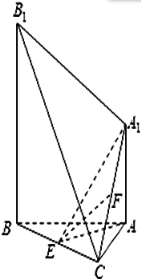
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】![]() 证明见解析;
证明见解析;![]()
![]()
【解析】
(1)由已知可得![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,从而
,从而![]() .故
.故![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
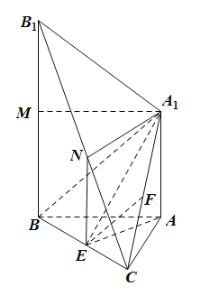
(2)取![]() 中点
中点![]() 和
和![]() 中点
中点![]() ,连接
,连接![]() ,可证四边形
,可证四边形![]() 为平行四边形,则
为平行四边形,则![]() ,且
,且![]() ,可证
,可证![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.又因为
所成的角.又因为![]() ,
,![]() ,有
,有![]() .故可求出
.故可求出![]() ,在在
,在在![]() 中,
中,![]() ,即可得到直线
,即可得到直线![]() 与平面
与平面![]() 所成角.
所成角.
解:(1)因为![]() ,
,![]() 为
为![]() 的中点.,所以
的中点.,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
从而![]() .
.
又因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() 和
和![]() 中点
中点![]() ,连接
,连接![]() .
.
因为![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的中点,所以
的中点,所以![]() (中位线定理),
(中位线定理),
故![]() ,故四边形
,故四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,且
,且![]() ,
,
又因为面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
从而![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
在![]() 中,可得
中,可得![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,
,
所以四边形![]() 是平行四边形
是平行四边形
所![]() ,
,![]() ,
,
又由![]() ,得
,得![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
因此![]() .
.
所以直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.


科目:高中数学 来源: 题型:
【题目】自2017年,大连“蜗享出行”正式引领共享汽车,改变人们传统的出行理念,给市民出行带来了诸多便利![]() 该公司购买了一批汽车投放到市场给市民使用
该公司购买了一批汽车投放到市场给市民使用![]() 据市场分析,每辆汽车的营运累计收入
据市场分析,每辆汽车的营运累计收入![]() 单位:元
单位:元![]() 与营运天数
与营运天数![]() 满足
满足![]() .
.
![]() 要使营运累计收入高于1400元求营运天数的取值范围;
要使营运累计收入高于1400元求营运天数的取值范围;
![]() 每辆汽车营运多少天时,才能使每天的平均营运收入最大?
每辆汽车营运多少天时,才能使每天的平均营运收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点到短轴的端点的距离为
的焦点到短轴的端点的距离为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,过点
两点,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:直线
,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中所有正确的序号是_________
①两直线的倾斜角相等,则斜率必相等;
②若动点![]() 到定点
到定点![]() 和定直线
和定直线![]() 的距离相等,则动点
的距离相等,则动点![]() 的轨迹是抛物线;
的轨迹是抛物线;
③已知![]() 、
、![]() 是椭圆
是椭圆![]() 的两个焦点,过点
的两个焦点,过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点,则
两点,则![]() 的周长为
的周长为![]() ;
;
④曲线的参数方程为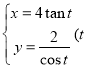 为参数
为参数![]() ,则它表示双曲线且渐近线方程为
,则它表示双曲线且渐近线方程为![]() ;
;
⑤已知正方形![]() ,则以
,则以![]() 、
、![]() 为焦点,且过
为焦点,且过![]() 、
、![]() 两点的椭圆的离心率为
两点的椭圆的离心率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,并且内切于定圆
,并且内切于定圆![]() .
.
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 上存在两个点
上存在两个点![]() ,
,![]() ,(1)中曲线上有两个点
,(1)中曲线上有两个点![]() ,
,![]() ,并且
,并且![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 其中a实数,e是自然对数的底数
其中a实数,e是自然对数的底数![]() .
.
![]() 1
1![]() 当
当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
![]() 2
2![]() 求
求![]() 在区间
在区间![]() 上的最小值;
上的最小值;
![]() 3
3![]() 若存在
若存在![]() ,
,![]() ,使方程
,使方程![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=3an+4,n∈N*.
(1)证明:数列{an+2}是等比数列,并求数列{an}的通项公式;
(2)设bn=(a2n+2)log3(an+2),求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com