
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)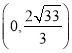
【解析】试题分析:(1)抛物线的焦点到准线的距离为![]() 可得
可得![]() ,从而得到抛物线的方程,然后设出切线切线
,从而得到抛物线的方程,然后设出切线切线![]() 的方程为
的方程为![]() ,由
,由![]() 求得
求得![]() ,由切点在抛物线上可得到
,由切点在抛物线上可得到![]() ,即为所求。(2)由(1)得到以线段
,即为所求。(2)由(1)得到以线段![]() 为直径的圆为圆
为直径的圆为圆![]() 。由题意只需考虑斜率为正数的直线
。由题意只需考虑斜率为正数的直线![]() 即可,根据几何知识得
即可,根据几何知识得![]() ,故
,故![]() 的方程为
的方程为![]() ,由弦长公式可得
,由弦长公式可得![]() ,又
,又![]() ,所以
,所以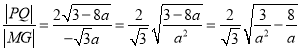 ,最后根据
,最后根据![]() 可得
可得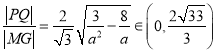 。
。
试题解析:
(1)由抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,得
,得![]() ,
,
则抛物线![]() 的方程为
的方程为![]() .
.
设切线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() ,
,
由![]() 得
得![]() ,
,
当![]() 时,点
时,点![]() 的横坐标为
的横坐标为![]() ,
,
则![]() ,
,
当![]() 时,同理可得
时,同理可得![]() .
.
综上得![]() 。
。
(2)由(1)知, ![]() ,
,
所以以线段![]() 为直径的圆为圆
为直径的圆为圆![]() ,
,
根据对称性,只要探讨斜率为正数的直线![]() 即可,
即可,
因为![]() 为直线
为直线![]() 与圆
与圆![]() 的切点,
的切点,
所以![]() ,
, ![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
由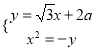 消去
消去![]() 整理得
整理得![]() ,
,
因为直线与圆相交,所以![]() 。
。
设![]() ,则
,则![]() ,
,
所以![]() ,
,
所以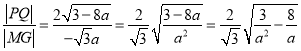 ,
,
设![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以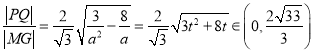 .
.


科目:高中数学 来源: 题型:
【题目】锐角△ABC中,其内角A,B满足:2cosA=sinB﹣ ![]() cosB.
cosB.
(1)求角C的大小;
(2)D为AB的中点,CD=1,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程是ρ=2,矩形ABCD内接于曲线C1 , A,B两点的极坐标分别为(2, ![]() )和(2,
)和(2, ![]() ),将曲线C1上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线C2 .
),将曲线C1上所有点的横坐标不变,纵坐标缩短为原来的一半,得到曲线C2 .
(1)写出C,D的直角坐标及曲线C2的参数方程;
(2)设M为C2上任意一点,求|MA|2+|MB|2+|MC|2+|MD|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温![]() (℃)与该小卖部的这种饮料销量
(℃)与该小卖部的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)据(1)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(℃),请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点O,焦点在x轴上,离心率为 ![]() ,椭圆C上的点到右焦点的最大距离为3.
,椭圆C上的点到右焦点的最大距离为3.
(1)求椭圆C的标准方程;
(2)斜率存在的直线l与椭圆C交于A,B两点,并且满足|2 ![]() +
+ ![]() |=|2
|=|2 ![]() ﹣
﹣ ![]() |,求直线在y轴上截距的取值范围.
|,求直线在y轴上截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣2sin2x+2 ![]() sinxcosx+1.
sinxcosx+1.
(1)求f(x)的最小正周期及对称中心;
(2)若x∈[﹣ ![]() ,
, ![]() ],求f(x)的最大值和最小值.
],求f(x)的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com