
已知函数 .
.
(1)求证函数 在区间
在区间 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应 的近似值(误差不超过
的近似值(误差不超过 );(参考数据
);(参考数据 ,
, ,
, )
)
(2)当 时,若关于
时,若关于 的不等式
的不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
解:(Ⅰ)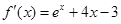 , ∵
, ∵ 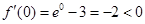 ,
,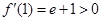 ,
,
∴ 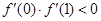 .
……………………2分
.
……………………2分
令 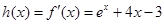 ,则
,则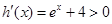 , ……………………3分
, ……………………3分
∴ 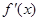 在区间
在区间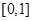 上单调递增,∴
上单调递增,∴ 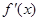 在区间
在区间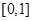 上存在唯一零点,
上存在唯一零点,
∴ 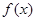 在区间
在区间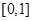 上存在唯一的极小值点. …………………………………4分
上存在唯一的极小值点. …………………………………4分
取区间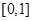 作为起始区间,用二分法逐次计算如下:
作为起始区间,用二分法逐次计算如下:
 ,而
,而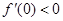 ,∴ 极值点所在区间是
,∴ 极值点所在区间是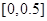 ;
;
又 ,∴ 极值点所在区间是
,∴ 极值点所在区间是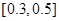 ;
;
③ ∵ 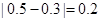 ,∴ 区间
,∴ 区间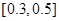 内任意一点即为所求. ……7分
内任意一点即为所求. ……7分
(Ⅱ)由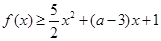 ,得
,得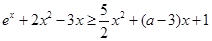 ,
,
即 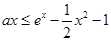 ,∵
,∵ 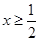 , ∴
, ∴ 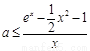 ,……………………8分
,……………………8分
令 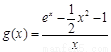 , 则
, 则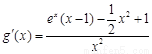 . ………………10分
. ………………10分
令 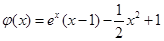 ,则
,则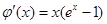 .
.
∵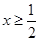 ,∴
,∴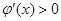 ,∴
,∴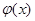 在
在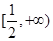 上单调递增,∴
上单调递增,∴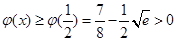 ,
,
因此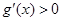 故
故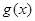 在
在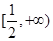 上单调递增,
……………………12分
上单调递增,
……………………12分
则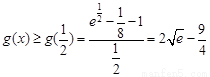 ,∴
,∴ 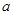 的取值范围是
的取值范围是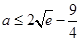 ………13分
………13分
【解析】略


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源:2011-2012学年人教版高一(上)期中数学试卷(解析版) 题型:解答题
 .
. 在(0,+∞)上是减函数.
在(0,+∞)上是减函数.查看答案和解析>>
科目:高中数学 来源:2010年上海市奉贤区高考数学二模试卷(文科)(解析版) 题型:解答题
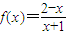 ;
; 成立,若存在求出x;若不存在,请说明理由.
成立,若存在求出x;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二下期中数学试卷(解析版) 题型:解答题
已知函数 令
令
(1)求 的定义域;
的定义域;
(2)判断函数 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(3)若 ,猜想
,猜想 之间的关系并证明.
之间的关系并证明.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市高三入学测试数学卷 题型:解答题
(本小题满分12分)
已知函数 ,
,
(1)求函数 的定义域;(2)证明:
的定义域;(2)证明: 是偶函数;
是偶函数;
(3)若 ,求
,求 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com