
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ),其部分图像如图所示.
),其部分图像如图所示.
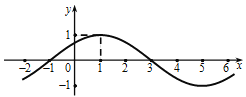
(1)求函数![]() 的解析式;
的解析式;
(2)已知横坐标分别为![]() 、
、![]() 、
、![]() 的三点
的三点![]() 都在函数
都在函数![]() 的图像上,求
的图像上,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线
(t为参数),以原点O为极点,x轴的非负半轴为极轴建立极坐标系,过极点的两射线![]() 、
、![]() 相互垂直,与曲线C分别相交于A、B两点(不同于点O),且
相互垂直,与曲线C分别相交于A、B两点(不同于点O),且![]() 的倾斜角为锐角
的倾斜角为锐角![]() .
.
(1)求曲线C和射线![]() 的极坐标方程;
的极坐标方程;
(2)求△OAB的面积的最小值,并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图象在
的图象在![]() 处取得极值4.
处取得极值4.
(1)求函数![]() 的单调区间;
的单调区间;
(2)对于函数![]() ,若存在两个不等正数
,若存在两个不等正数![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,则把区间
,则把区间![]() 叫函数
叫函数![]() 的“正保值区间”.问函数
的“正保值区间”.问函数![]() 是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
是否存在“正保值区间”,若存在,求出所有的“正保值区间”;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据养殖规模与以往的养殖经验,某海鲜商家的海产品每只质量(克)在正常环境下服从正态分布![]() .
.
(1)随机购买10只该商家的海产品,求至少买到一只质量小于![]() 克该海产品的概率.
克该海产品的概率.
(2)2020年该商家考虑增加先进养殖技术投入,该商家欲预测先进养殖技术投入为49千元时的年收益增量.现用以往的先进养殖技术投入![]() (千元)与年收益增量
(千元)与年收益增量![]() (千元)(
(千元)(![]() )的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线
)的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且
的附近,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,其中
,其中![]() ,
,![]() =
=![]()
![]() .根据所给的统计量,求
.根据所给的统计量,求![]() 关于
关于![]() 的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
附:若随机变量![]() ,则
,则![]() ,
,![]() ;
;
对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为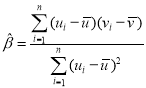 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,点
,点![]() ,过
,过![]() 的直线
的直线![]() 与圆
与圆![]() 交于点
交于点![]() ,过
,过![]() 做直线
做直线![]() 平行
平行![]() 交
交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过![]() 的直线与
的直线与![]() 交于
交于![]() 、
、![]() 两点,若线段
两点,若线段![]() 的中点为
的中点为![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.命题“![]() ,
,![]() ”是假命题
”是假命题
C.若命题![]() 、
、![]() 均为假命题,则命题
均为假命题,则命题![]() 为真命题
为真命题
D.若![]() 是定义在R上的函数,则“
是定义在R上的函数,则“![]() ”是“
”是“![]() 是奇函数”的必要不允分条件
是奇函数”的必要不允分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com