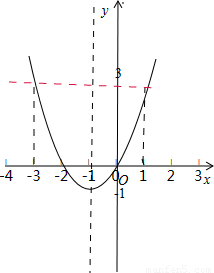Question

已知函数y=x²+2x在闭区间[a，b]上的值域为[-1，3]，则满足题意的有序实数对（a，b）在坐标平面内所对应点组成图形的长度为    ．

Answer 1

【答案】分析：由已知函数y=x²+2x在闭区间[a，b]上的值域为[-1，3]，画出图象可得a、b满足的条件，进而可求出答案．
解答：解：∵y=（x+1）²-1，∴可画出图象如图所示．
由x²+2x=3，解得x=-3或x=1；又当x=-1时，（-1）²-2=-1．
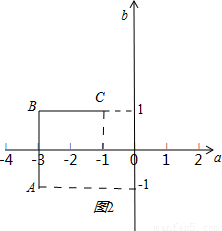
①当a=-3时，b必须满足-1≤b≤1，可得点（a，b）在坐标平面内所对应点组成图形的长度为|AB|=1-（-1）=2；
②当-3＜a≤-1时，b必须满足b=1，可得点（a，b）在坐标平面内所对应点组成图形的长度为|BC|=（-1）-（-3）=2．
如图2所示：∴|AB|+|BC|=2+2=4．
故答案为4．



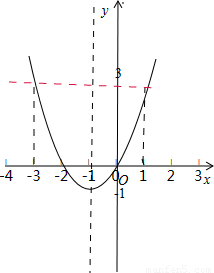点评：本题综合考查了二次函数的单调性和值域，充分理解和利用其单调性及数形结合的思想方法是解决问题的关键．