
【题目】设函数![]() .
.
(1)求函数的单调区间;
(2)若![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(3)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求证:数列
),求证:数列![]() 是等比数列;
是等比数列;
⑵若数列![]() 是等比数列,求
是等比数列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近期前期广告投入量![]() (单位:万元)和收益
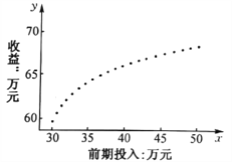
(单位:万元)和收益![]() (单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共
(单位:万元)的数据。对这些数据作了初步处理,得到了下面的散点图(共![]() 个数据点)及一些统计量的值.为了进一步了解广告投入量
个数据点)及一些统计量的值.为了进一步了解广告投入量![]() 对收益
对收益![]() 的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
的影响,公司三位员工①②③对历史数据进行分析,查阅大量资料,分别提出了三个回归方程模型:
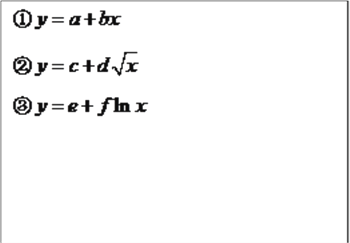
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据![]() ,
, ![]() ,参考数据:
,参考数据: ![]() ,
, ![]() .
.
(1)根据散点图判断,哪一位员工提出的模型不适合用来描述![]() 与
与![]() 之间的关系?简要说明理由.
之间的关系?简要说明理由.
(2)根据(1)的判断结果及表中数据,在余下两个模型中分别建立收益![]() 关于投入量
关于投入量![]() 的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益
的关系,并从数据相关性的角度考虑,在余下两位员工提出的回归模型中,哪一个是最优模型(即更适宜作为收益![]() 的回归方程)?说明理由;
的回归方程)?说明理由;
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率、截距的最小二乘估计以及相关系数分别为:
的斜率、截距的最小二乘估计以及相关系数分别为:
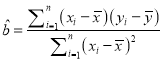 ,
, ![]() ,
, 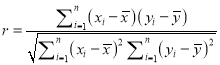 ,
,
其中![]() 越接近于
越接近于![]() ,说明变量
,说明变量![]() 与
与![]() 的线性相关程度越好.
的线性相关程度越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的椭圆或双曲线的标准方程:
(1)椭圆的焦点在![]() 轴上,焦距为4,且经过点
轴上,焦距为4,且经过点![]() ;
;
(2)双曲线的焦点在![]() 轴上,右焦点为
轴上,右焦点为![]() ,过
,过![]() 作重直于
作重直于![]() 轴的直线交双曲线于
轴的直线交双曲线于![]() ,
,![]() 两点,且
两点,且![]() ,离心率为
,离心率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 及点
及点![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,且
,且![]() (
( ![]() 为坐标原点),椭圆
为坐标原点),椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查:人类在能源利用与森林砍伐中使CO2浓度增加.据测,2015年,2016年,2017年大气中的CO2浓度分别比2014年增加了1个单位,3个单位,6个单位.若用一个函数模拟每年CO2浓度增加的单位数y与年份增加数x的关系,模拟函数可选用二次函数![]() (其中
(其中![]() 为常数)或函数
为常数)或函数![]() (其中a,b,c为常数),又知2018年大气中的CO2浓度比2014年增加了16.5个单位,请问用以上哪个函数作模拟函数较好?
(其中a,b,c为常数),又知2018年大气中的CO2浓度比2014年增加了16.5个单位,请问用以上哪个函数作模拟函数较好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com