
【题目】设向量 ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(
=( ![]() cosx,﹣
cosx,﹣ ![]() ),函数f(x)=(
),函数f(x)=( ![]() +
+ ![]() )
) ![]() .
.
(1)求函数f(x)的单调递增区间;
(2)当x∈(0, ![]() )时,求函数f(x)的值域.
)时,求函数f(x)的值域.
【答案】
(1)解:∵ ![]() =(sinx,﹣1),
=(sinx,﹣1), ![]() =(
=( ![]() cosx,﹣
cosx,﹣ ![]() ),
),
∴f(x)=( ![]() +
+ ![]() )
) ![]() =(sinx+
=(sinx+ ![]() cosx,﹣
cosx,﹣ ![]() )(sinx,﹣1)
)(sinx,﹣1)
=sin2x+ ![]() sinxcos+
sinxcos+ ![]() =
= ![]() (1﹣cos2x)+
(1﹣cos2x)+ ![]() sin2x+
sin2x+ ![]()
= ![]() sin2x﹣
sin2x﹣ ![]() cos2x)+2
cos2x)+2
=sin(2x﹣ ![]() )+2,
)+2,
由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,
,
解得:kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
故函数的递增区间是[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ]
]
(2)解:∵x∈(0, ![]() ),
),
∴2x﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),
),
故sin(2x﹣ ![]() )的最大值是1,sin(2x﹣
)的最大值是1,sin(2x﹣ ![]() )>sin(﹣
)>sin(﹣ ![]() )=﹣
)=﹣ ![]() ,
,
故函数的最大值是3,最小值大于 ![]() ,
,
即函数的值域是( ![]() ,3]
,3]
【解析】(1)利用向量数量积公式化简函数,结合正弦函数的单调增区间,可得f(x)的单调增区间;(2)求出(2x﹣ ![]() )的范围,从而确定f(x)的范围,化简函数,可得函数的值域.
)的范围,从而确定f(x)的范围,化简函数,可得函数的值域.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a1=1,前n项和Sn满足条件 ![]() =4,n=1,2,…
=4,n=1,2,…
(1)求数列{an}的通项公式和Sn;
(2)记bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在高二年级开设选修课,其中数学选修课开了三个班.选课结束后,有四名选修英语的同学要求改修数学,但数学选修每班至多可再接收两名同学,那么安排好这四名同学的方案有( )
A.72种
B.54种
C.36种
D.18种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°, ![]() ,D为AC上一点,且AD=3DC.
,D为AC上一点,且AD=3DC. 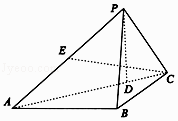
(1)求证:PD⊥平面ABC;
(2)若E为PA中点,求直线CE与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在[0,+∞)上是增函数,g(x)=﹣f(|x|),若g(lgx)>g(1),则x的取值范围是( )
A.(0,10)
B.(10,+∞)
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2x2+bx+c,不等式f(x)<0的解集为(0,5).
(1)求b,c的值;
(2)若对任意x∈[﹣1,1],不等式f(x)+t≤2恒成立,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A,B,C的对边长分别为a,b,c,R是△ABC的外接圆半径,有下列四个条件: ⑴(a+b+c)(a+b﹣c)=3ab
⑵sinA=2cosBsinC
⑶b=acosC,c=acosB
⑷ ![]()
有两个结论:甲:△ABC是等边三角形.乙:△ABC是等腰直角三角形.
请你选取给定的四个条件中的两个为条件,两个结论中的一个为结论,写出一个你认为正确的命题 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x﹣2y+3=0和l2:x+2y﹣9=0的交点为A.
(1)求过点A,且与直线2x+3y﹣1=0平行的直线方程;
(2)求过点A,且倾斜角为直线l1倾斜角2倍的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com