

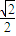 :
: =OH:3,∴OH=
=OH:3,∴OH=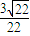 ,
,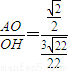 =
=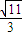 ,∠AHO=arctan
,∠AHO=arctan .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
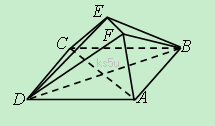
(09年长沙一中第八次月考理)(本小题满分12分)如图,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EF//AC,∠CAF=∠AFE=90º,AB=![]() ,AF=FE=1.
,AF=FE=1.
(1)求证EC//平面BDF;
(2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
(04年浙江卷理)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=![]() ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
(1)求证AM//平面BDE;
(2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与BC所成的角是60°。

查看答案和解析>>
科目:高中数学 来源: 题型:

(1)(理)求证:AM∥平面BDE;
(文)求证:AM⊥平面BDF1;
(2)求二面角A-DF-B的大小;
(3)(理)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年新人教版高三上学期单元测试(6)数学试卷 题型:选择题
(理)已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂
直于ABCD所在的平面,且GC=2,点B到平面EFG的距离为 ( )
A. B.
B.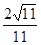 C.
C.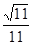 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com