练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】执行如图的程序框图，则输出的s=（　　）

    A.
    B.-
    C.
    D.-

    【答案】B
    【解析】解：由题意，模拟执行程序，可得
    α=12°，s=1
    s=cos12°，α=24°
    不满足条件α＞180°，s=cos12°cos24°，α=48°，
    不满足条件α＞180°，s=cos12°cos24°cos48°，α=96°，
    不满足条件α＞180°，s=cos12°cos24°cos48°cos96°，α=192°，
    满足条件α＞180°，退出循环，输出s=cos12°cos24°cos48°cos96°，α=192°，
    由于s=cos12°cos24°cos48°cos96°
    =﹣sin6°cos12°cos24°cos48°



    =﹣ ．
    故选：B．
    解答算法框图的问题，要依次执行各个步骤，特别注意循环结构的终止条件，本题中是α＞180°就终止循环，可得s=cos12°cos24°cos48°cos96°，给原式的分子分母都乘以24cos6°，然后分子连续利用四次二倍角的正弦函数公式后再利用诱导公式把正弦化为余弦，约分即可得解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax3﹣bx2+cx+b﹣a（a＞0）．
    （1）设c=0． ①若a=b，曲线y=f（x）在x=x0处的切线过点（1，0），求x0的值；
    ②若a＞b，求f（x）在区间[0，1]上的最大值．
    （2）设f（x）在x=x1 ， x=x2两处取得极值，求证：f（x1）=x1 ， f（x2）=x2不同时成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx+bx﹣c，f（x）在点（1，f（1））处的切线方程为x+y+4=0．
    （1）求f（x）的解析式；
    （2）求f（x）的单调区间；
    （3）若在区间 内，恒有f（x）≥2lnx+kx成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}．满足：an+1＞an（n∈N*），a1=1，该数列的前三项分别加上1，1，3后成等比数列，an+2log2bn=﹣1．
    （Ⅰ）分别求数列{an}，{bn}的通项公式；
    （Ⅱ）求数列{anbn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在定义域内既是奇函数又是减函数的是（　　）
    A.y=
    B.y=﹣x+
    C.y=﹣x|x|
    D.y=

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C过点，且与圆外切于点，是x轴上的一个动点．

    求圆C的标准方程；

    当圆C上存在点Q，使，求实数m的取值范围；

    当时，过P作直线PA，PB与圆C分别交于异于点P的点A，B两点，且求证：直线AB恒过定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知 AF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=2，AB=4．
    （I）求证：AC⊥平面BCE；
    （II）求三棱锥E﹣BCF的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥P﹣ABCD的底面为菱形，∠BCD=120°，AB=PC=2，AP=BP= ．

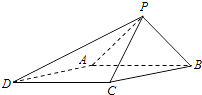
    （1）求证：AB⊥PC；
    （2）求二面角B一PC﹣D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD－A1B1C1D1中，M，N，P分别是C1C, C1B1，C1D1的中点，点H在四边形A1ADD1的边及其内部运动，则H满足条件________时，有BH∥平面MNP.

    查看答案和解析>>

    同步练习册答案