
| 患慢性气管炎 | 未患慢性气管炎 | 总计 | |
| 吸烟 | 360 | 320 | 680 |
| 不吸烟 | 140 | 180 | 320 |
| 合计 | 500 | 500 | 1000 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:山东省济宁市2012届高三第一次高考模拟数学理科试题 题型:044
某高中社团进行社会实验,对[25,55]岁的人群随机抽取1000人进行了一次是否开通“微博”的调查,若开通“微博”的为“时尚族”,否则称为“非时尚族”.通过调查得到各年龄段人数的频率分布直方图如图所示,其中在[40,45)岁、[45,50)岁年龄段人数中,“时尚族”人数分别占本组人数的40%、30%.
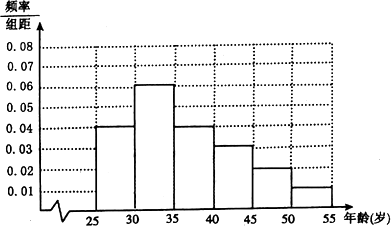
请完成以下问题:
(Ⅰ)求[40,45)岁与[45,50)岁年龄段“时尚族”的人数;
(Ⅱ)从[40,45)岁和[45,50)岁年龄段的“时尚族”中,采用分层抽样法抽取9人参加网络时尚达人大赛,其中选取3人作为领队,已选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源:2013届黑龙江省高二期末考试文科数学试卷(解析版) 题型:解答题
调查1000名50岁以上有吸烟习惯与患慢性气管炎的人的情况,获数据如下表:
|
|
患慢性气管炎 |
未患慢性气管炎 |
总计 |
|
吸烟 |
360 |
320 |
680 |
|
不吸烟 |
140 |
180 |
320 |
|
合计 |
500 |
500 |
1000 |
试问:根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为吸烟习惯与患慢性气管炎病有关?参考数据如下:
(k=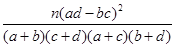 ,且P(K2≥6.635)≈0.01,)
,且P(K2≥6.635)≈0.01,)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济南一中高三(下)4月质量检测数学试卷(理科)(解析版) 题型:解答题
| 组数 | 分组 | 低碳族 的人数 | 占本组 的频率 |
| 1 | [25,30) | 120 | 0.6 |
| 2 | [30,35) | 195 | P |
| 3 | [35,40) | 100 | 0.5 |
| 4 | [40,45) | a | 0.4 |
| 5 | [45,50) | 30 | 0.3 |
| 6 | [50,55) | 15 | 0.3 |
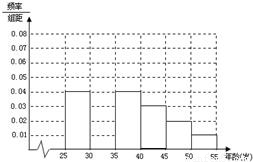
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com