
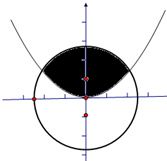
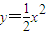 将圆面x2+y2≤8分成两部分,现在向圆面上均匀投点,这些点落在图中阴影部分的概率为
将圆面x2+y2≤8分成两部分,现在向圆面上均匀投点,这些点落在图中阴影部分的概率为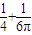 ,则定积分
,则定积分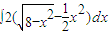 = .
= .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 抛物线y=
抛物线y=| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6π |
| ∫ | 2 0 |
| 8-x2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 下列四个命题中,真命题的序号有
下列四个命题中,真命题的序号有| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年山东卷理)下列四个命题中,真命题的序号有 (写出所有真命题的序号).
①将函数y=![]() 的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=
的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=![]()
②圆x2+y2+4x-2y+1=0与直线y=![]() 相交,所得弦长为2
相交,所得弦长为2
③若sin(![]() +
+![]() )=
)=![]() ,sin(
,sin(![]() -
-![]() )=
)=![]() ,则tan
,则tan![]() cot
cot![]() =5
=5
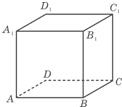
④如图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.

(16题图)
查看答案和解析>>
科目:高中数学 来源: 题型:
①将函数y=|x+1|的图象按向量v=(-1,0)平移,得到的图象对应的函数表达式为y=|x|
②圆x2+y2+4x+2y+1=0与直线y=![]() x相交,所得弦长为2
x相交,所得弦长为2
③若sin(α+β)=![]() ,sin(α-β)=
,sin(α-β)=![]() ,则tanαcotβ=5
,则tanαcotβ=5
④如图,已知正方体ABCD—A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分

查看答案和解析>>
科目:高中数学 来源: 题型:
①将函数y=|x+1|的图象按向量v=(-1,0)平移,得到的图象对应的函数表达式为y=|x|
②圆x2+y2+4x+2y+1=0与直线y=![]() x相交,所得弦长为2
x相交,所得弦长为2
③若sin(α+β)=![]() ,sin(α-β)=
,sin(α-β)=![]() ,则tanαcotβ=5
,则tanαcotβ=5
④如图,已知正方体ABCD-A1B

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com