练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (1)设α为锐角，试比较sin2α和sin(α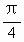＋)的大小；

    (2)已知θ∈(0，2π)且sinθcos2θ＞0，求θ的范围．

    答案：
    解析：

    　　解 (1)分别画出y＝sin2α(0＜α＜)和y＝sin(α＋)(0＜α＜)的图象．由图象易得sin2α≤sin(α＋)．

    　　(2)解法1 (Ⅰ)由cos2θ＞0＜2θ＜2π或0≤2θ＜(舍)或＜θ＜π或0≤θ＜(舍去θ＝0)，它们都满足sinθ＞0．(Ⅱ)仿(Ⅰ)，即(舍)，∴满足条件的θ的范围是(0，． 

    　　解法2 转化为sinθ(sinθ－)(sinθ＋)＜0．由序轴法知－1≤sinθ＜－或0＜sinθ＜，得θ∈∪．


    提示：

    注 (1)的比较大小，可用作差法，然后和差化积解之．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆C：
    x2
    m2
    +
    y2
    n2
    =1(0＜m＜n)    的离心率为
    		3
    2
    ，且经过点P(
    		3
    2
    ，1)    ．
    （1）求椭圆C的方程；
    （2）设直线l：y=kx+t（k≠0）交椭圆C于A、B两点，D为AB的中点，kOD为直线OD的斜率，求证：k•kOD为定值；
    （3）在（2）条件下，当t=1时，若
    OA
    与
    OB
    的夹角为锐角，试求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    设α、β均为锐角，试寻找(1＋tanα)(1＋tanβ)＝2成立的充要条件，并化简

    (1＋tan)(1＋tan)…(1＋tan)(1＋tan)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

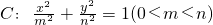    已知椭圆数学公式的离心率为数学公式，且经过点数学公式．
    （1）求椭圆C的方程；
    （2）设直线l：y=kx+t（k≠0）交椭圆C于A、B两点，D为AB的中点，kOD为直线OD的斜率，求证：k•kOD为定值；
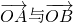    （3）在（2）条件下，当t=1时，若数学公式的夹角为锐角，试求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011年山东省潍坊市高三摸底数学试卷（文科）（解析版） 题型：解答题

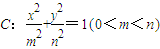    已知椭圆的离心率为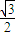，且经过点．
    （1）求椭圆C的方程；
    （2）设直线l：y=kx+t（k≠0）交椭圆C于A、B两点，D为AB的中点，kOD为直线OD的斜率，求证：k•kOD为定值；
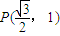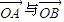    （3）在（2）条件下，当t=1时，若的夹角为锐角，试求k的取值范围．

    查看答案和解析>>

    同步练习册答案