【题目】从某校高中男生中随机选取100名学生，将他们的体重（单位： 
）数据绘制成频率分布直方图，如图所示．
（1）估计该校的100名同学的平均体重（同一组数据以该组区间的中点值作代表）；
（2）若要从体重在
， 
， 
三组内的男生中，用分层抽样的方法选取6人组成一个活动队，再从这6人中选2人当正副队长，求这2人中至少有1人体重在
内的概率．
【答案】（1）
（2）
【解析】试题分析：（1）每个小矩形的中点横坐标与纵坐标的积之和就是该校的
名同学的平均体重；（2）记体重在
的
人为
， 
， 
， 
的
人为
， 
， 
的1人为
，利用列举法求出总事件个数为
种，符合条件的事件个数为
，利用古典概型概率公式可得结果.
试题解析：（1）估计该校的100名同学的平均体重为：
．
（2）由频率分布直方图可知体重在
， 
， 
三组内的男生人数分别为
， 
， 
，
故这三组中通过分层抽样所抽取的人数分别为3,2,1．
记体重在
的3人为
， 
， 
， 
的2人为
， 
， 
的1人为
，
则从这6人中抽取2人的所有可能结果为： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
共15种，
其中体重在
至少有1人的结果有： 
， 
， 
， 
， 
， 
， 
， 
， 
共9种，故这2人中至少有1人体重在
内的概率为
．
科目：高中数学 来源： 题型：
【题目】甲、乙两名同学准备参加考试，在正式考试之前进行了十次模拟测试，测试成绩如下：
甲：137，121，131，120，129，119，132，123，125，133
乙：110，130，147，127，146，114，126，110，144，146
（1）画出甲、乙两人成绩的茎叶图，求出甲同学成绩的平均数和方差，并根据茎叶图，写出甲、乙两位同学平均成绩以及两位同学成绩的中位数的大小关系的结论；
（2）规定成绩超过127为“良好”，现在老师分别从甲、乙两人成绩中各随机选出一个，求选出成绩“良好”的个数
的分布列和数学期望.
(注：方差
，其中
为
的平均数）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】对于各项均为整数的数列
，如果满足
（
）为完全平方数，则称数列
具有“
性质”；不论数列
是否具有“
性质”，如果存在与
不是同一数列的
，且
同时满足下面两个条件：①
是
的一个排列；②数列
具有“
性质”，则称数列
具有“变换
性质”.
（Ⅰ）设数列
的前
项和
，证明数列
具有“
性质”；
（Ⅱ）试判断数列
和数列
是否具有“变换
性质”，具有此性质的数列请写出相应的数列
，不具此性质的说明理由；
（Ⅲ）对于有限项数列
，某人已经验证当
（
）时，数列
具有“变换
性质”，试证明：当
时，数列
也具有“变换
性质”.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为调查银川市某校高中生是否愿意提供志愿者服务，用简单随机抽样方法从该校调查了50人，结果如下：
（1）用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人，其中男生抽取多少人？
（2）在（1）中抽取的6人中任选2人，求恰有一名女生的概率；
（3）你能否在犯错误的概率不超过0.010的前提下，认为该校高中生是否愿意提供志愿者服务与性别有关？
下面的临界值表供参考：
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
独立性检验统计量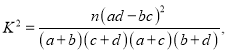
其中
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某化工厂为预测产品的回收率
，需要研究它和原料有效成分含量
之间的相关关系，现收集了4组对照数据。
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
（Ⅰ）请根据相关系数
的大小判断回收率
与
之间是否存在高度线性相关关系；
（Ⅱ）请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
，并预测当
时回收率
的值.
参考数据： 
| 1 | 0 |
|
| 其他 |
| 完全相关 | 不相关 | 高度相关 | 低度相关 | 中度相关 |
， 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左右焦点分别为
， 
上的动点
到两焦点的距离之和为4，当点运动到椭圆的上顶点时，直线
恰与以原点
为圆心，以椭圆的离心率为半径的圆相切.
（1）求椭圆的方程；
（2）设椭圆的左右顶点分别为
，若
交直线
于
两点.问以
为直径的圆是否过定点？若过定点，请求出该定点坐标；若不过定点，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中错误的是__________（填序号）
①命题“
，有
”的否定是“
”，有
”；
②已知
， 
， 
，则
的最小值为
；
③设
，命题“若
，则
”的否命题是真命题；
④已知
， 
，若命题
为真命题，则
的取值范围是
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某单位的职工食堂中，食堂每天以
元/个的价格从面包店购进面包，然后以
元/个的价格出售．如果当天卖不完，剩下的面包以
元/个的价格全部卖给饲料加工厂．根据以往统计资料，得到食堂每天面包需求量的频率分布直方图如下图所示．食堂某天购进了80个面包，以
（单位：个，
）表示面包的需求量，
（单位：元）表示利润．
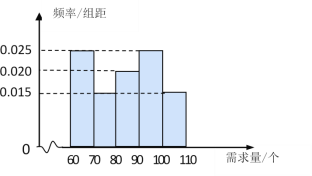
（1）求关于的函数解析式；
（2）根据直方图估计利润不少于
元的概率；
（3）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如：若需求量
，则取
，且的概率等于需求量落入
的频率)，求的分布列和数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
