【题目】在数列
中，
，
，
（1）设
，证明：数列
是等差数列；
（2）求数列的前
项和.
【答案】（1）证明见解析；（2）
.
【解析】
试题分析：（1）由
，可得
，化简得
，即可证明；（2）由（1）可得：
，
，再利用“错位相减法”、等比数列的前
项和公式即可得出.
试题解析：(1)证明 由已知an＋1＝2an＋2n，
得
.
，又
.
∴{bn}是首项为1，公差为1的等差数列．
(2)解 由(1)知，bn＝n，
.∴an＝n·2n－1.
∴Sn＝1＋2·21＋3·22＋…＋n·2n－1
两边乘以2得：2Sn＝1·21＋2·22＋…＋(n－1)·2n－1＋n·2n，
两式相减得：－Sn＝1＋21＋22＋…＋2n－1－n·2n
＝2n－1－n·2n＝(1－n)2n－1，
∴Sn＝(n－1)·2n＋1.
永乾教育寒假作业快乐假期延边人民出版社系列答案科目：高中数学 来源： 题型：
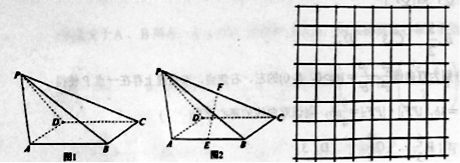
【题目】如图1，在四棱锥
中，底面
是正方形，
．
（1）如图2，设点
为
的中点，点
为
的中点，求证:
平面
；
（2）已知网格纸上小正方形的边长为
，请你在网格纸上用粗线画图1中四棱锥的府视图（不需要标字母），并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市要建成宜商、宜居的国际化新城，该城市的东城区、西城区分别引进8个厂家，现对两个区域的16个厂家进行评估，综合得分情况如茎叶图所示.
（1）根据茎叶图判断哪个区域厂家的平均分较高；
（2）规定85分以上（含85分）为优秀厂家，若从该两个区域各选一个优秀厂家，求得分差距不超过5分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获
（单位：
）与它的“相近”作物株数
之间的关系如下表所示：
| 1 | 2 | 3 | 4 |
| 51 | 48 | 45 | 42 |
这里，两株作物“相近”是指它们之间的直线距离不超过1米．
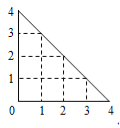
（1）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰好“相近”的概率；
（2）在所种作物中堆积选取一株，求它的年收获量的分布列与数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知：以点
(
)为圆心的圆与
轴交
于点O, A，与y轴交于点O, B，其中O为原点．
（1）求证：△OAB的面积为定值；
（2）设直线
与圆C交于点M, N，若OM = ON，求圆C的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆：
，点
.
（1）设
是椭圆
上任意的一点，
是点
关于坐标原点的对称点，记
，求
的取值范围；
（2）已知点
，
，
是椭圆
上在第一象限内的点，记
为经过原点与点
的直线，
为
截直线
所得的线段长，试将
表示成直线
的斜率
的函数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】记
表示
，
中的最大值，如
．已知函数
，
．
（1）设
，求函数
在
上零点的个数；
（2）试探讨是否存在实数
，使得
对
恒成立？若存在，求
的取值范围；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
