
已知函数 (
( ).
).
(1)若 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;
(2)若对任意的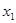 ,
,
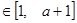 ,总有
,总有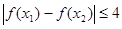 ,求实数
,求实数 的取值范围.
的取值范围.
(1)  ; (2)
; (2) 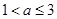 .
.
解析试题分析:(1)首先用配方法求出二次函数 的对称轴为
的对称轴为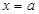 ,由于
,由于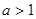 ,知函数
,知函数 在已知区间
在已知区间 是为减函数,要使函数定义域和值域均为
是为减函数,要使函数定义域和值域均为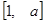 ,必须且只需
,必须且只需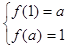 ,从而得到关于a的方程组,解此方程组得实数
,从而得到关于a的方程组,解此方程组得实数 的值;(2)因为对任意的
的值;(2)因为对任意的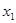 ,
,
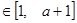 ,总有
,总有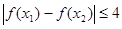 ,等价于:
,等价于: ,所以问题转化为求函数
,所以问题转化为求函数 在
在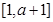 的最大值和最小值;由于二次函数
的最大值和最小值;由于二次函数 的开口向上,且对称轴为
的开口向上,且对称轴为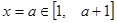 ,所以其最小值一定是
,所以其最小值一定是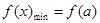 ,而最大值就是两个端点值所对函数值中的较大者,由二次函数的性质可知:等价于比较两个区间的端点谁离对称轴远些;由此只需按
,而最大值就是两个端点值所对函数值中的较大者,由二次函数的性质可知:等价于比较两个区间的端点谁离对称轴远些;由此只需按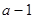 与1的大小进行分类讨论,即可用a的代数式表示出函数
与1的大小进行分类讨论,即可用a的代数式表示出函数 在
在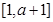 的最大值和最小值,然后代入
的最大值和最小值,然后代入 就可求得a的取值范围.
就可求得a的取值范围.
试题解析:(1)∵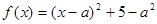 (
(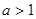 ),
),
∴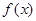 在
在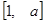 上是减函数,又定义域和值域均为
上是减函数,又定义域和值域均为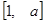 ,∴
,∴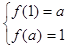 ,
,
即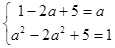 , 解得
, 解得  .
.
(2)若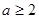 ,又
,又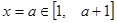 ,且
,且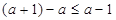 ,
,
∴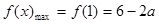 ,
,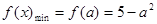 .
.
∵对任意的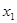 ,
,
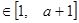 ,总有
,总有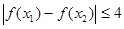 ,
,
∴ , 即
, 即 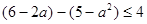 ,解得
,解得 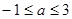 ,
,
又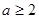 , ∴
, ∴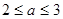 .
.
若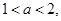
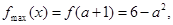
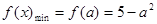 ,
, 显然成立,
显然成立,
综上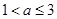 .
.
考点:1.二次函数的单调性与最值;2.分类讨论.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD、AB距离分别为9m,3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN:NE=16:9.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1)用x的代数式表示AM,并写出x的取值范围;
(2)求S关于x的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 =
=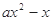 (
( ,
,
(1)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(2)若函数 与
与 的图像有两个不同的交点
的图像有两个不同的交点 ,求
,求 的取值范围。
的取值范围。
(3)设点 和
和 (
( 是函数
是函数 图像上的两点,平行于
图像上的两点,平行于 的切线以
的切线以 为切点,求证
为切点,求证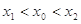 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市环保部门对市中心每天环境污染情况进行调查研究,发现一天中环境污染指数 与时刻
与时刻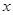 (时)的关系为
(时)的关系为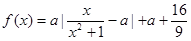 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且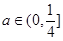 ,用每天
,用每天 的最大值作为当天的污染指数,记作
的最大值作为当天的污染指数,记作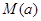 .
.
(1)令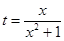 ,
, ,求
,求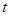 的取值范围;
的取值范围;
(2)按规定,每天的污染指数不得超过2,问目前市中心的污染指数是否超标?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地需要修建一条大型输油管道通过240公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为400万元,铺设距离为 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为 万元.设余下工程的总费用为
万元.设余下工程的总费用为 万元.
万元.
(1)试将 表示成
表示成 的函数;
的函数;
(2)需要修建多少个增压站才能使 最小,其最小值为多少?
最小,其最小值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果n件产品中任取一件样品是次品的概率为 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
).
(1)求该企业日赢利额 的最大值;
的最大值;
(2)为保证每天的赢利额不少于日赢利额最大值的50%,试求该企业日产量的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)的图象与函数h(x)=x+ +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+ ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com