Question

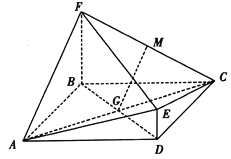
【题目】如图，菱与四边形BDEF相交于BD， 平面ABCD，DE//BF,BF=2DE，AF⊥FC，M为CF的中点， ．

(I)求证：GM／／平面CDE；

(II)求证：平面ACE⊥平面ACF．

Answer 1

【答案】(1)详见解析;(2)详见解析.

【解析】试题分析:(1) 取的中点，连接.由，又因为，且，所以平面平面，又平面，所以平面;(2) 连接，由.设菱形的边长为2，则， ，则， ，且平面， ，得平面，又，所以， 平面，又平面，所以平面平面.

试题解析:证明：（Ⅰ）取的中点，连接.

因为为菱形对角线的交点，所以为中点，所以，又因为分别为

的中点，所以，又因为，所以，又，

所以平面平面，

又平面，所以平面；

（Ⅱ）证明：连接，因为四边形为菱形，

所以，又平面，所以，

所以.

设菱形的边长为2， ，

则，

又因为，所以，

则， ，且平面， ，得平面，

在直角三角形中， ，

又在直角梯形中，得，

从而，所以，又，

所以平面，又平面，

所以平面平面.

点睛:直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行,即线线平行推出线面平行.两平面垂直的判定有两种方法:(1)两个平面所成的二面角是直角；(2)一个平面经过另一平面的垂线．掌握基本的判定和性质定理外还应理解线线、线面、面面垂直的转化思想，逐步学会综合运用数学知识分析解决问题的能力.