
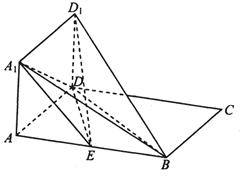
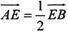 时,求二面角D1-EC-D的大小.
时,求二面角D1-EC-D的大小.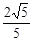 (3)D1-EC-D的大小为
(3)D1-EC-D的大小为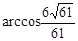

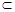 面A1DE,BD1
面A1DE,BD1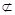 面A1DE,
面A1DE,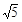 ,
,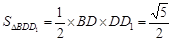 ,
,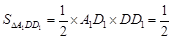 ,
,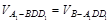 有
有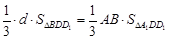 ,即
,即 ,解得
,解得 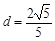 ,
,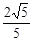 .……………………………………………8分
.……………………………………………8分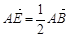 ,有
,有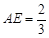 ,
,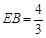 ,
,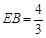 ,BC=1,得
,BC=1,得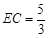 .又DH·EC=DC·BC,代入解得
.又DH·EC=DC·BC,代入解得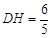 ,
,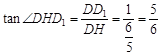 .∴
.∴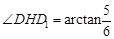 ,即二面角D1-EC-D的大小为
,即二面角D1-EC-D的大小为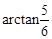 .…………12分
.…………12分
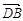 =(1,2,0),
=(1,2,0),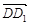 =(0,0,1),
=(0,0,1),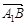 =(0,2,-1).设面BDD1的一个法向量为n1
=(0,2,-1).设面BDD1的一个法向量为n1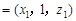 ,
,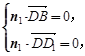 即
即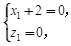 ∴
∴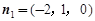 .
.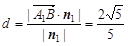 . …………………………8分
. …………………………8分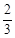 ,0),C(0,2,0),
,0),C(0,2,0),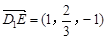 ,
,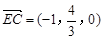 .
.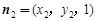 ,
,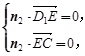 即
即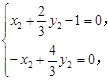 可得
可得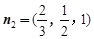 .
. (0,0,1),
(0,0,1),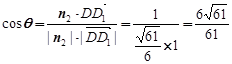 ,得
,得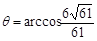 .
.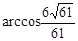


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:填空题
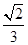 a,则MN与平面BB1C1C的位置关系是________.
a,则MN与平面BB1C1C的位置关系是________.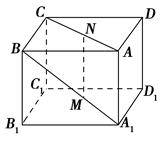
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,使得平面
,使得平面 ⊥平面ABD.
⊥平面ABD.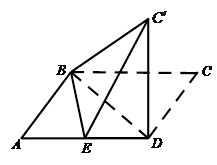
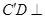 平面ABD;
平面ABD;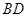 与平面
与平面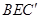 所成角的正弦值;
所成角的正弦值; 的余弦值.
的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
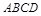 中,
中,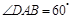 .点
.点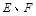 分别在边
分别在边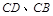 上,点
上,点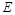 与点
与点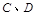 不重合,
不重合,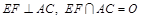 .沿
.沿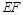 将
将 翻折到
翻折到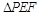 的位置,使平面
的位置,使平面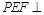 平面
平面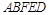 .
.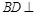 平面
平面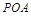 ;
;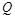 满足
满足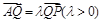 ,试探究:当
,试探究:当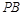 取得最小值时,直线
取得最小值时,直线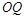 与平面
与平面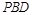 所成角的大小是否一定大于
所成角的大小是否一定大于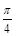 ?并说明理由.
?并说明理由.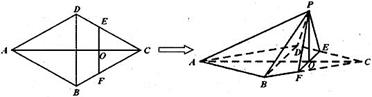
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
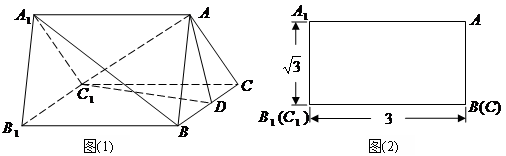
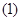 是一个水平放置的正三棱柱
是一个水平放置的正三棱柱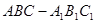 ,
,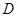 是棱
是棱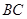 的中点.正三棱柱的主视图如图
的中点.正三棱柱的主视图如图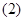 .
.
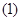 中垂直于平面
中垂直于平面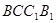 的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)
的平面有哪几个?(直接写出符合要求的平面即可,不必说明或证明)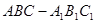 的体积;
的体积;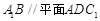 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com