
【题目】某中学举行了一次“环保只知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为![]() 分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.
分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.

(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到广场参加环保只是的志愿宣传活动.
名同学到广场参加环保只是的志愿宣传活动.
1)求所抽取的![]() 名同学中至少有
名同学中至少有![]() 名同学来自第
名同学来自第![]() 组的概率;
组的概率;
2)求所抽取的![]() 名同学来自同一组的概率.
名同学来自同一组的概率.
【答案】(1) ![]() ,
, ![]() ;(2)1)
;(2)1) ![]() ;2)
;2) ![]() .
.
【解析】试题分析:(1)利用频率分布表和频率分布直方图,由题意能求出a,b,x,y的值;(2)(ⅰ)由题意可知,第4组共有4人,记为A,B,C,D,第5组共有2人,记为X,Y.从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学,有15种情况由此能求出随机抽取的2名同学中至少有1名同学来自第5组的概率;(ⅱ)设“随机抽取的2名同学来自同一组”为事件F,有AB,AC,AD,BC,BD,CD,XY共7种情况,由此能求出随机抽取的2名同学来自同一组的概率.
试题解析:
(1)由题意可知,样本总人数为![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() .
.
(2)1)由题意可知,第![]() 组共有
组共有![]() 人,记为
人,记为![]() ,第
,第![]() 组共有
组共有![]() 人,记为
人,记为![]() .从竞赛成绩是
.从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中抽取
分)的同学中抽取![]() 名同学有
名同学有![]() ,
, ![]() ,
, ![]() 共
共![]() 种情况.设“随机抽取的
种情况.设“随机抽取的![]() 名同学中至少有
名同学中至少有![]() 名同学来自第
名同学来自第![]() 组”为事件
组”为事件![]() ,有
,有![]() 共
共![]() 种情况.所以
种情况.所以![]() .即随机抽取的
.即随机抽取的![]() 名同学中至少有
名同学中至少有![]() 名同学来自第
名同学来自第![]() 组的概率是
组的概率是![]() .
.
2)设“随机抽取的![]() 名同学来自同一组”为事件
名同学来自同一组”为事件![]() ,有
,有![]() 共
共![]() 种情况.所以
种情况.所以![]() .即随机抽取的
.即随机抽取的![]() 名同学来自同一组的概率是
名同学来自同一组的概率是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 与
与![]() 的中心在原点,焦点分别在
的中心在原点,焦点分别在![]() 轴与
轴与![]() 轴上,它们有相同的离心率
轴上,它们有相同的离心率![]() ,并且
,并且![]() 的短轴为
的短轴为![]() 的长轴,
的长轴,![]() 与
与![]() 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是![]() .
.
(1)求椭圆![]() 与
与![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上非顶点的动点,
上非顶点的动点,![]() 与椭圆
与椭圆![]() 长轴两个顶点
长轴两个顶点![]() ,
,![]() 的连线
的连线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
,![]() 点.
点.
(i)求证:直线![]() ,
,![]() 斜率之积为常数;
斜率之积为常数;
(ii)直线![]() 与直线
与直线![]() 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() =
= ![]() ,
, ![]() =(4sinx,cosx﹣sinx),f(x)=
=(4sinx,cosx﹣sinx),f(x)= ![]()
![]() .
.
(1)求函数f(x)的解析式;
(2)已知常数ω>0,若y=f(ωx)在区间 ![]() 是增函数,求ω的取值范围;
是增函数,求ω的取值范围;
(3)设集合A= ![]() ,B={x||f(x)﹣m|<2},若AB,求实数m的取值范围.
,B={x||f(x)﹣m|<2},若AB,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 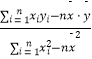 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,当x>0时,f′(x)sinx+f(x)cosx>0且f( ![]() )=1,则f(x)sinx≤1的整数解的集合为 .
)=1,则f(x)sinx≤1的整数解的集合为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图甲所示,据此解答如下问题: 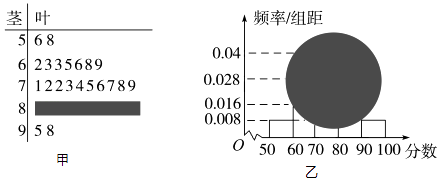
(1)求该班全体男生的人数;
(2)求分数在[80,90)之间的男生人数,并计算频率公布直方图如图乙中[80,90)之间的矩形的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面α及直线a,b,则下列说法正确的是( )
A.若直线a,b与平面α所成角都是30°,则这两条直线平行
B.若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直
C.若直线a,b平行,则这两条直线中至少有一条与平面α平行
D.若直线a,b垂直,则这两条直线与平面α不可能都垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题。
(1)求函数f(x)=x2﹣2x+2.在区间[ ![]() ,3]上的最大值和最小值;
,3]上的最大值和最小值;
(2)已知f(x)=ax3+bx﹣4,若f(2)=6,求f(﹣2)的值
(3)计算0.0081 ![]() +(4
+(4 ![]() )2+(
)2+( ![]() )
) ![]() ﹣16﹣0.75+3
﹣16﹣0.75+3 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com