练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知圆C的圆心在直线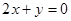上，并经过A，两点。

     (1)求圆C的方程。

    (2)若直线l与圆C相切，且在x轴和y轴上的截距相等，求直线l的方程；

    (3)已知，从圆C外一点P(x，y)向圆引一条切线，切点为M. 且有|PM|＝|PD|，求使得|PM|取得最小值的点P的坐标.

     

    【答案】

     (1)圆C的方程：。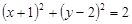

    (2)直线l的方程为x＋y＋1＝0或x＋y－3＝0或y=(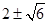)x.

    (3) P点坐标为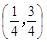

    【解析】本试题主要是考查了直线与圆的位置关系的综合运用。

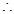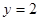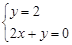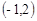    （1）线段AB是圆C的弦，AB的中垂线必过圆心，由解得圆心C，半径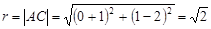，可得到圆的方程。

    （2）由于圆心坐标C(－1,2)，半径r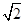＝，当切线在两坐标轴上的截距相等且不为零时．设直线l的方程为x＋y＝a，∵直线l与圆C相切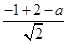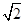，∴＝，∴a＝－1或a＝3. ∴直线l的方程为x＋y＋1＝0或x＋y－3＝0；。

    （3）∵切线PM与半径CM垂直，设P(x，y)，又∵|PM|2＝|PC|2－|CM|2，|PM|＝|PD|

    然后用坐标表示线段长，进而得到轨迹方程。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知圆C的圆心在直线x-3y=0上，且圆C与x轴相切，若圆C截直线y=x得弦长为2
    		7
    ，求圆C的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C的圆心在直线y=x+1上，且过点A（1，3），与直线x+2y-7=0相切．
    （1）求圆C的方程；
    （2）设直线l：ax-y-2=0（a＞0）与圆C相交于A、B两点，求实数a的取值范围；
    （3）在（Ⅱ）的条件下，是否存在实数a，使得弦AB的垂直平分线l过点P（-2，4），若存在，求出实数a的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C的圆心在直线y=2x上，且与直线l：x+y+1=0相切于点P（-1，0）．
    （Ⅰ）求圆C的方程；
    （Ⅱ）若A（1，0），点B是圆C上的动点，求线段AB中点M的轨迹方程，并说明表示什么曲线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C的圆心在直线2x-y-3=0上，且经过点A（5，2），B（3，2），
    （1）求圆C的标准方程；
    （2）直线l过点P（2，1）且与圆C相交的弦长为2
    		6
    ，求直线l的方程．
    （3）设Q为圆C上一动点，O为坐标原点，试求△OPQ面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C的圆心在直线l1：x-y-1=0上，与直线l2：4x+3y+14=0相切，且截得直线l3：3x+4y+10=0所得弦长为6，求圆C的方程．

    查看答案和解析>>

    同步练习册答案