
【题目】已知函数f(x)=sin(x+![]() )+sin(x﹣
)+sin(x﹣![]() )+cosx.
)+cosx.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)在△ABC中,f(A)=![]() ,△ABC的面积为
,△ABC的面积为![]() ,AB=
,AB=![]() ,求BC的长.
,求BC的长.
【答案】(Ⅰ)![]() (Ⅱ)2或
(Ⅱ)2或![]()
【解析】
(1)先根据两角和与差正弦公式展开,再根据配角公式得基本三角函数形式,最后根据正弦函数周期公式求结果,(2)先求A,再根据面积公式求不,最后根据余弦定理求a.
函数f(x)=sin(x+![]() )+sin(x﹣
)+sin(x﹣![]() )+cosx.
)+cosx.
化简可得:f(x)=2sinxcos![]() +cosx=
+cosx=![]() sinx+cosx=2sin(x+
sinx+cosx=2sin(x+![]() )
)
(Ⅰ)f(x)的最小正周期T=![]() ;
;
(Ⅱ)由f(A)=![]() ,即2sin(A+
,即2sin(A+![]() )=
)=![]() ,
,
∴sin(A+![]() )=
)=![]() ,
,
∵0<A<π,
∴![]() <(A+
<(A+![]() )
)![]() .
.
可得:(A+![]() )=
)=![]() 或
或![]()
则A=![]() 或A=
或A=![]() .
.
当则A=![]() 时,△ABC的面积为
时,△ABC的面积为![]() =
=![]() bcsinA,AB=c=
bcsinA,AB=c=![]() ,
,
∴b=AC=2
余弦定理:BC2=22+(2![]() )2﹣2×
)2﹣2×![]() ×cos
×cos![]() ,
,
解得:BC=2
当A=![]() 时,△ABC的面积为
时,△ABC的面积为![]() =
=![]() bc,AB=c=
bc,AB=c=![]() ,
,
∴b=AC=1
直角三角形性质可得:BC2=22+(2![]() )2,
)2,
解得:BC=![]() .
.
故答案为:2或![]()


科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,点
,点![]() 是圆
是圆![]() 上的一个动点,点
上的一个动点,点![]()
![]() 分别在线段
分别在线段![]()
![]() 上,且满足
上,且满足![]() ,
,![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 与点
与点![]() 的轨迹相交于
的轨迹相交于![]() 两点,在
两点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一级品;当
时,产品为一级品;当![]() 时,产品为二级品,当
时,产品为二级品,当![]() 时,产品为三级品,现用两种新配方(分别称为
时,产品为三级品,现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做实验,各生产了
配方)做实验,各生产了![]() 件这种产品,并测量了每件产品的质量指标值,得到下面的试验结果 :(以下均视频率为概率)
件这种产品,并测量了每件产品的质量指标值,得到下面的试验结果 :(以下均视频率为概率)
![]() 配方的频数分配表:
配方的频数分配表:
指标值分组 |
|
|
|
|
频数 |
|
|
|
|
![]() 配方的频数分配表:
配方的频数分配表:
指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)若从![]() 配方产品中有放回地随机抽取
配方产品中有放回地随机抽取![]() 件,记“抽出的
件,记“抽出的![]() 配方产品中至少
配方产品中至少![]() 件二级品”为事件
件二级品”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;
;
(2)若两种新产品的利润率![]() 与质量指标
与质量指标![]() 满足如下关系:
满足如下关系: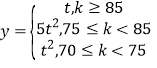 ,其中
,其中![]() ,从长期来看,投资哪种配方的产品平均利润率较大?
,从长期来看,投资哪种配方的产品平均利润率较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高衡水市的整体旅游服务质量,市旅游局举办了旅游知识竞赛,参赛单位为本市内各旅游协会,参赛选手为持证导游.现有来自甲旅游协会的导游3名,其中高级导游2名;乙旅游协会的导游3名,其中高级导游1名.从这6名导游中随机选择2人参加比赛.
(1)求选出的2名都是高级导游的概率;
(2)为了进一步了解各旅游协会每年对本地经济收入的贡献情况,经多次统计得到,甲旅游协会对本地经济收入的贡献范围是![]() (单位:万元),乙旅游协会对本地经济收入的贡献范围是
(单位:万元),乙旅游协会对本地经济收入的贡献范围是![]() (单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献概率.
(单位:万元),求甲旅游协会对本地经济收入的贡献不低于乙旅游协会对本地经济收入的贡献概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)由0,1,2,…,9这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于7的四位数的个数共有几种?
(2)我校高三学习雷锋志愿小组共有16人,其中一班、二班、三班、四班各4人,现在从中任选3人,要求这三人不能是同一个班级的学生,且在三班至多选1人,求不同的选取法的种数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
,![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() 为真命题”是“
为真命题”是“![]() ”的必要不充分条件,求正整数
”的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com