

 解:设圆锥的底面半径为r,高为h,体积为V,那么r2+h2=R2,
解:设圆锥的底面半径为r,高为h,体积为V,那么r2+h2=R2, πr2h
πr2h π(R2-h2)h=
π(R2-h2)h= πR2h-
πR2h- πh3(0<h<R).…(3分)
πh3(0<h<R).…(3分) πR2-πh2.
πR2-πh2. πR2-πh2=0,得 h=
πR2-πh2=0,得 h= R.…(5分)
R.…(5分) R时,V'>0.
R时,V'>0. R<h<R时,V'<0.
R<h<R时,V'<0. R时,V取得极大值,并且这个极大值是最大值.…(8分)
R时,V取得极大值,并且这个极大值是最大值.…(8分)  R代入r2+h2=R2,得 r=
R代入r2+h2=R2,得 r= R.
R. π.
π. .
.

 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
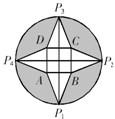 如图,从一个半径为(1+
如图,从一个半径为(1+| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第19期 总175期 人教课标高一版 题型:013
如图所示,从一个半径为1+![]() m的圆形纸板中切割出一块图形,该图形的中间是正方形,四周是以正方形各边为底边的四个正三角形,将其折叠成一个正四棱锥P-ABCD,则该正四棱锥的体积是
m的圆形纸板中切割出一块图形,该图形的中间是正方形,四周是以正方形各边为底边的四个正三角形,将其折叠成一个正四棱锥P-ABCD,则该正四棱锥的体积是

![]() m3
m3
![]() m3
m3
![]() m3
m3
![]() m3
m3
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省宿迁市高二(上)期末数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com