
【题目】已知数列{an}的前n项和Sn , 且an= ![]() (n∈N*). (Ⅰ)若数列{an+t}是等比数列,求t的值;
(n∈N*). (Ⅰ)若数列{an+t}是等比数列,求t的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)记bn= ![]() +
+ ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】解:(Ⅰ)当n=1时,由a1= ![]() (n∈N*),得a1=1.
(n∈N*),得a1=1.
当n≥2时,an=sn﹣sn﹣1=2an﹣n﹣2an﹣1+(n﹣1),
即an=2an﹣1+1,∴a2=3,a3=7,.
依题意,得(3+t)2=(1+t)(7+t),解得t=1,
当t=1时,an+1=2(an﹣1+1),n≥2,
即数列{an+1}是等比数列,故实数t的值为1.
(Ⅱ)由(Ⅰ),知当n≥2时,an+1=2(an﹣1+1),
又因为a1+1=2,
所以数列{an+1}是以2为首项,2为公比的等比数列.
所以 ![]() ,
,
∴a ![]() (n∈N+).
(n∈N+).
(Ⅲ)由(Ⅱ),知bn= ![]() +
+ ![]() =
= ![]() =
= 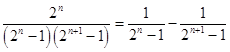 ,
,
则Tn= ![]() =1﹣
=1﹣ ![]()
【解析】(Ⅰ)易得an=2an﹣1+1,∴a2=3,a3=7,依题意,得(3+t)2=(1+t)(7+t),解得t=1, (Ⅱ)由(Ⅰ),知当n≥2时,an+1=2(an﹣1+1),即数列{an+1}是以2为首项,2为公比的等比数列,得 ![]() ,即可求通项.(Ⅲ)由(Ⅱ),知bn=
,即可求通项.(Ⅲ)由(Ⅱ),知bn= ![]() +
+ ![]() =
= ![]() =
= ![]() ,累加即可求和.
,累加即可求和.
【考点精析】通过灵活运用等比数列的通项公式(及其变式)和数列的前n项和,掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系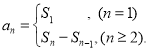 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】函数f(x)同时满足①f(x)为偶函数;②对任意x,有f( ![]() ﹣x)=f(
﹣x)=f( ![]() +x),则函数f(x)的解析式可以是( )
+x),则函数f(x)的解析式可以是( )
A.f(x)=cos2x
B.![]()
C.f(x)=cos6x
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 且 ![]() =
= ![]() ,a1=m,现有如下说法: ①a2=5;
,a1=m,现有如下说法: ①a2=5;
②当n为奇数时,an=3n+m﹣3;
③a2+a4+…+a2n=3n2+2n.
则上述说法正确的个数为( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 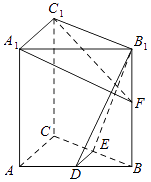
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为 . 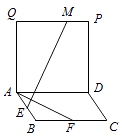
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD= ![]() ,PA=AD=2,AB=BC=1.
,PA=AD=2,AB=BC=1. 
(1)求平面PAB与平面PCD所成二面角的余弦值;
(2)点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( ) 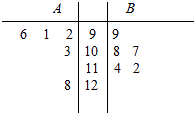
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com