
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为
,上顶点为![]() ,
,![]() 的面积为1,且椭圆
的面积为1,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 在椭圆上且位于第二象限,过点
在椭圆上且位于第二象限,过点![]() 作直线
作直线![]() ,过点
,过点![]() 作直线
作直线![]() ,若直线
,若直线![]() 的交点
的交点![]() 恰好也在椭圆
恰好也在椭圆![]() 上,求点
上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)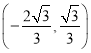
【解析】
(1)根据题设条件,列出![]() 的方程组,结合
的方程组,结合![]() ,求得
,求得![]() 的值,即可得到椭圆的标准方程;
的值,即可得到椭圆的标准方程;
(2)设![]() ,分
,分![]() 和
和![]() 两种情况讨论,当
两种情况讨论,当![]() 时,联立
时,联立![]() 的方程组,取得
的方程组,取得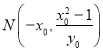 ,再结合椭圆的对称性,列出方程组,即可求解
,再结合椭圆的对称性,列出方程组,即可求解
(1)由椭圆![]() 的上顶点为
的上顶点为![]() ,
,![]() 的面积为1,且椭圆
的面积为1,且椭圆![]() 的离心率为
的离心率为![]() ,
,
可得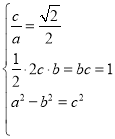 ,解得
,解得![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由(1)知,椭圆的方程![]() ,可得
,可得![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() .
.
当![]() 时,
时,![]() 与
与![]() 相交于点
相交于点![]() 不符合题意;
不符合题意;
当![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
因为![]() ,
,![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立![]() 和
和![]() 的方程,解得
的方程,解得![]() ,
,![]() ,所以
,所以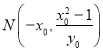 ,
,
因为点![]() 在椭圆
在椭圆![]() 上,由椭圆的对称性,可知
上,由椭圆的对称性,可知![]() ,
,
所以![]() 或
或![]() ,
,
由方程组 ,解得
,解得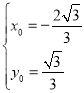 ,而方程组
,而方程组 无解(舍去),
无解(舍去),
所以点![]() 的坐标为
的坐标为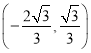 .
.


科目:高中数学 来源: 题型:
【题目】设f(x),g(x)分别是定义在R上的奇函数和偶函数,f′(x),g'(x)为其导函数,当x<0时,f′(x)![]() g(x)+f(x)
g(x)+f(x)![]() g'(x)<0且g(﹣3)=0,则使得不等式f(x)
g'(x)<0且g(﹣3)=0,则使得不等式f(x)![]() g(x)<0成立的x的取值范围是( )
g(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣3)B.(﹣3,0)C.(0,3)D.(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是边长
是边长![]() ,
,![]() 的矩形硬纸片,在硬纸片的四角切去边长相等的小正方形后,再沿虚线折起,做成一个无盖的长方体盒子,
的矩形硬纸片,在硬纸片的四角切去边长相等的小正方形后,再沿虚线折起,做成一个无盖的长方体盒子,![]() 、
、![]() 是
是![]() 上被切去的小正方形的两个顶点,设
上被切去的小正方形的两个顶点,设![]() .
.

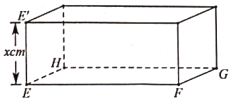
(1)将长方体盒子体积![]() 表示成
表示成![]() 的函数关系式,并求其定义域;
的函数关系式,并求其定义域;
(2)当![]() 为何值时,此长方体盒子体积
为何值时,此长方体盒子体积![]() 最大?并求出最大体积.
最大?并求出最大体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市近郊有一块大约![]() 的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为
的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为![]() 平方米.
平方米.
(1)分别用![]() 表示
表示![]() 和
和![]() 的函数关系式,并给出定义域;
的函数关系式,并给出定义域;
(2)怎样设计能使![]() 取得最大值,并求出最大值.
取得最大值,并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
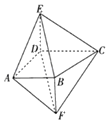
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R,关于x的方程(x2﹣ax+1)(x2﹣bx+1)=0的四个实根构成以q为公比的等比数列,若q∈[![]() ,2],则ab的取值范围为______.
,2],则ab的取值范围为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() .
.
(1)令![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() 成立?若存在,求出所有
成立?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,侧面PDC是正三角形,平面PDC⊥平面ABCD,CD=2,M为PB的中点.

(1)求证:PA⊥平面CDM.
(2)求二面角D-MC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种智能手机的投入成本是4500元/部,当手机售价为6000元/部时,月销售量为![]() 台,市场分析的结果表明,如果手机的销售价提高的百分率为
台,市场分析的结果表明,如果手机的销售价提高的百分率为![]() ,那么月销售量减少的百分率为
,那么月销售量减少的百分率为![]() .记销售价提高的百分率为
.记销售价提高的百分率为![]() 时,月利润是
时,月利润是![]() 元.
元.
(1)写出月利润![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如何确定这种智能手机的销售价,使得该公司的月利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com