
【题目】已知函数f(x)=xlnx﹣ ![]() x2﹣x+a,a∈R
x2﹣x+a,a∈R
(1)当a=0时,求函数f(x)的极值;
(2)若函数f(x)在其定义域内有两个不同的极值点(极值点是指函数取极值时对应的自变量的值),记为x1 , x2 , 且x1<x2 . (ⅰ)求a的取值范围;
(ⅱ)若不等式e1+λ<x1x ![]() 恒成立,求正实数λ的取值范围.
恒成立,求正实数λ的取值范围.
【答案】
(1)解:a=0时,f(x)=xlnx﹣x,函数的定义域是(0,+∞),
f(x)=lnx,令f′(x)>0,解得:x>1,令f′(x)<0,解得:0<x<1,
故函数在(0,1)递减,在(1,+∞)递增,
故函数的极小值是f(1)=﹣1
(2)解:(i)由题意知,函数f(x)的定义域为(0,+∞),
方程f′(x)=0在(0,+∞)有两个不同根;
即方程lnx﹣ax=0在(0,+∞)有两个不同根;
(解法一)转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,
如右图.
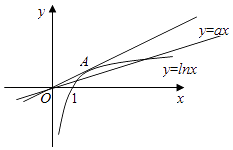
可见,若令过原点且切于函数y=lnx图象的直线斜率为k,只须0<a<k.
令切点A(x0,lnx0),
故k=y′|x=x0= ![]() ,又k=
,又k= ![]() ,
,
故 ![]() =
= ![]() ,解得,x0=e,
,解得,x0=e,
故k= ![]() ,故0<a<
,故0<a< ![]() .
.
(解法二)转化为函数g(x)= ![]() 与函数y=a的图象在(0,+∞)上有两个不同交点
与函数y=a的图象在(0,+∞)上有两个不同交点
又g′(x)= ![]() ,
,
即0<x<e时,g′(x)>0,x>e时,g′(x)<0,
故g(x)在(0,e)上单调增,在(e,+∞)上单调减.
故g(x)极大=g(e)= ![]() ;
;
又g(x)有且只有一个零点是1,且在x→0时,g(x)→﹣∞,在在x→+∞时,g(x)→0,
故g(x)的草图如右图,
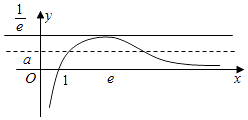
可见,要想函数g(x)= ![]() 与函数y=a的图象在(0,+∞)上有两个不同交点,
与函数y=a的图象在(0,+∞)上有两个不同交点,
只须0<a< ![]() .
.
(解法三)令g(x)=lnx﹣ax,从而转化为函数g(x)有两个不同零点,
而g′(x)= ![]() ﹣ax=
﹣ax= ![]() (x>0),
(x>0),
若a≤0,可见g′(x)>0在(0,+∞)上恒成立,所以g(x)在(0,+∞)单调增,
此时g(x)不可能有两个不同零点.
若a>0,在0<x< ![]() 时,g′(x)>0,在x>
时,g′(x)>0,在x> ![]() 时,g′(x)<0,
时,g′(x)<0,
所以g(x)在(0, ![]() )上单调增,在(
)上单调增,在( ![]() ,+∞)上单调减,从而g(x)极大值=g(
,+∞)上单调减,从而g(x)极大值=g( ![]() )=ln
)=ln ![]() ﹣1,
﹣1,
又因为在x→0时,g(x)→﹣∞,在在x→+∞时,g(x)→﹣∞,
于是只须:g(x)极大>0,即ln ![]() ﹣1>0,所以0<a<
﹣1>0,所以0<a< ![]() .
.
综上所述,0<a< ![]() .
.
(ii)因为e1+λ<x1x2λ等价于1+λ<lnx1+λlnx2.
由(i)可知x1,x2分别是方程lnx﹣ax=0的两个根,
即lnx1=ax1,lnx2=ax2
所以原式等价于1+λ<ax1+λax2=a(x1+λx2),因为λ>0,0<x1<x2,
所以原式等价于a> ![]() ,
,
又由lnx1=ax1,lnx2=ax2作差得,ln ![]() =a(x1﹣x2),
=a(x1﹣x2),
即a=  ,所以原式等价于
,所以原式等价于  >
> ![]() ,
,
因为0<x1<x2,原式恒成立,即ln ![]() <
< ![]() 恒成立,
恒成立,
令t= ![]() ,t∈(0,1),
,t∈(0,1),
则不等式lnt< ![]() 在t∈(0,1)上恒成立.
在t∈(0,1)上恒成立.
令h(t)=lnt﹣ ![]() ,
,
又h′(t)=  ,
,
当λ2≥1时,可见t∈(0,1)时,h′(t)>0,
所以h(t)在t∈(0,1)上单调增,又h(1)=0,h(t)<0在t∈(0,1)恒成立,符合题意.
当λ2<1时,可见t∈(0,λ2)时,h′(t)>0,t∈(λ2,1)时h′(t)<0,
所以h(t)在t∈(0,λ2)时单调增,在t∈(λ2,1)时单调减,又h(1)=0,
所以h(t)在t∈(0,1)上不能恒小于0,不符合题意,舍去.
综上所述,若不等式e1+λ<x1x2λ恒成立,只须λ2≥1,又λ>0,所以λ≥1
【解析】(1)求出f(x)的解析式,求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极小值即可;(2)(i)由导数与极值的关系知可转化为方程f′(x)=lnx﹣ax=0在(0,+∞)有两个不同根;再转化为函数y=lnx与函数y=ax的图象在(0,+∞)上有两个不同交点,或转化为函数g(x)= ![]() 与函数y=a的图象在(0,+∞)上有两个不同交点;或转化为g(x)=lnx﹣ax有两个不同零点,从而讨论求解;(ii)e1+λ<x1x2λ可化为1+λ<lnx1+λlnx2,结合方程的根知1+λ<ax1+λax2=a(x1+λx2),从而可得a>
与函数y=a的图象在(0,+∞)上有两个不同交点;或转化为g(x)=lnx﹣ax有两个不同零点,从而讨论求解;(ii)e1+λ<x1x2λ可化为1+λ<lnx1+λlnx2,结合方程的根知1+λ<ax1+λax2=a(x1+λx2),从而可得a> ![]() ;而a=
;而a= ![]() ,从而可得ln
,从而可得ln ![]() <恒成立;再令t=
<恒成立;再令t= ![]() ,t∈(0,1),从而可得不等式lnt<
,t∈(0,1),从而可得不等式lnt< ![]() 在t∈(0,1)上恒成立,再令h(t)=lnt﹣
在t∈(0,1)上恒成立,再令h(t)=lnt﹣ ![]() ,从而利用导数化恒成立问题为最值问题即可.
,从而利用导数化恒成立问题为最值问题即可.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】有一容量为50的样本,数据的分组以及各组的频数如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),5;[30.5,33.5],4.
(1)列出样本的频率分布表.
(2)画出频率分布直方图.
(3)根据频率分布表,估计数据落在[15.5,24.5)内的可能性约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是某池塘中的浮萍蔓延的面积![]() 与时间
与时间![]() 月)的关系
月)的关系![]() 有以下叙述:
有以下叙述:
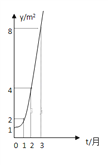
①这个指数函数的底数是2;
②第5个月时,浮萍的面积就会超过![]()
③浮萍从![]() 蔓延到
蔓延到![]() 需要经过1.5个月;
需要经过1.5个月;
④浮萍每个月增加的面积都相等;
⑤若浮萍蔓延到![]() 所经过的时间分别为
所经过的时间分别为![]() 则
则![]() .其中正确的是
.其中正确的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近来景德镇市棚户区改造进行的如火如荼,加上城市人居环境的不断改善,我市房地产住宅销售价格节节攀升,一部分刚需住户带来了不小的烦恼,下表为我市2017.1﹣2017.5这5月住宅价格与月份的关系.
月份x | 1 | 2 | 3 | 4 | 5 |
住宅价格y | 4.8 | 5.4 | 6.2 | 6.6 | 7 |
(1)通过计算线性相关系数判断住宅价y千元/平米与月份x的线性相关程度(精确到0.01)
(2)用最小二乘法得到的线性回归直线去近似拟合x,y的关系. ①求y关于x的回归方程;②试估计按照这个趋势下去,将在不久的哪个年月份,房价将突破万元/平米的大关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一只蚂蚁绕一个竖直放置的圆环逆时针匀速爬行,已知圆环的半径为8![]() ,圆环的圆心
,圆环的圆心![]() 距离地面的高度为10
距离地面的高度为10![]() ,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点
,蚂蚁每12分钟爬行一圈,若蚂蚁的起始位置在最低点![]() 处.
处.
(1)试确定在时刻![]() (
(![]() )时蚂蚁距离地面的高度
)时蚂蚁距离地面的高度![]() ;
;
(2)在蚂蚁绕圆环爬行的一圈内,有多长时间蚂蚁距离地面超过14![]() ?
?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数![]() 是偶函数,且满足
是偶函数,且满足![]() 上的解析式为
上的解析式为![]() ,过点
,过点![]() 作斜率为k的直线l,若直线l与函数
作斜率为k的直线l,若直线l与函数![]() 的图象至少有4个公共点,则实数k的取值范围是
的图象至少有4个公共点,则实数k的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(甲),在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如图(乙).
,如图(乙).
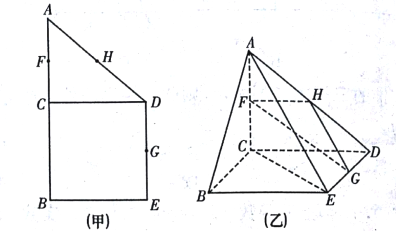
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口水的深度![]() 是时间
是时间![]() ,单位:
,单位: ![]() 的函数,记作
的函数,记作![]() .下面是某日水深的数据:
.下面是某日水深的数据:

经长期观察, ![]() 的曲线可以近似地看成函数
的曲线可以近似地看成函数![]() 的图象.一般情况下,船舶航行时,船底离海底的距离为
的图象.一般情况下,船舶航行时,船底离海底的距离为![]() 或
或![]() 以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
(1)求![]() 与
与![]() 满足的函数关系式;
满足的函数关系式;
(2)某船吃水程度(船底离水面的距离)为![]() ,如果该船希望在同一天内安全进出港,请问它同一天内最多能在港内停留多少小时?(忽略进出港所需的时间).
,如果该船希望在同一天内安全进出港,请问它同一天内最多能在港内停留多少小时?(忽略进出港所需的时间).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com