
设函数f(x)=  ×
× ,其中向量
,其中向量 ="(2cosx,1),"
="(2cosx,1),"  =(cosx,
=(cosx, sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和f(x)在[0, p]上的单调递增区间;
(2)当xÎ[0, ]时,ô f(x)ô <4恒成立,求实数m的取值范围.
]时,ô f(x)ô <4恒成立,求实数m的取值范围.
(1) T=p, [0, ],[
],[ , p] (2) -4<m<1.
, p] (2) -4<m<1.
解析试题分析:(1)f(x)=  ×
× =2cos2x+
=2cos2x+ sin2x+m 1分
sin2x+m 1分
=cos2x+ sin2x+m+1=2sin(2x+
sin2x+m+1=2sin(2x+ )+m+1 3分
)+m+1 3分
∴f(x)的最小正周期T=p, 4分
在[0, p]上的单调递增区间为[0, ],[
],[ ,p] 6分
,p] 6分
(2)∵当xÎ[0, ]时,
]时,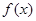 递增,当xÎ[
递增,当xÎ[ ,
, ]时,
]时,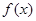 递减,
递减,
∴当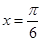 时,
时,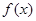 的最大值等于
的最大值等于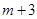 . 8分
. 8分
当x= 时,
时,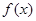 的最小值等于m. 10分
的最小值等于m. 10分
由题设知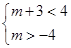 解之得,-4<m<1. 12分
解之得,-4<m<1. 12分
考点:本题考查了三角函数的性质及最值
点评:三角函数最值问题是历年高考重点考查的知识点之一,它不仅与三角自身的常见基础知识如三角函数概念、图象和性质,诱导公式,同角关系式,两角和与差的三角公式等密切相关


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com