
【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0, ![]() )的图象如图所示.
)的图象如图所示. 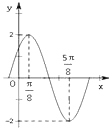
(1)求A,w及φ的值;
(2)若tana=2,求 ![]() 的值.
的值.
【答案】
(1)解:由图知A=2,
T=2( ![]() )=p,
)=p,
∴w=2,
∴f(x)=2sin(2x+φ)
又∵ ![]() =2sin(
=2sin( ![]() +φ)=2,
+φ)=2,
∴sin( ![]() +φ)=1,
+φ)=1,
∴ ![]() +j=
+j= ![]() ,φ=
,φ= ![]() +2kπ,
+2kπ,
∵ ![]() ,
,
∴φ= ![]()
(2)解:由(1)知:f(x)=2sin(2x+ ![]() ),
),
∴ ![]() =2sin(2a+
=2sin(2a+ ![]() )=2cos2a=4cos2a﹣2
)=2cos2a=4cos2a﹣2
∵tana=2,
∴sina=2cosa,
又∵sin2a+cos2a=1,
∴cos2a= ![]() ,
,
∴ ![]() =
= ![]()
【解析】(1)根据函数图象的最大值和最小值确定A的值,由周期可知ω的值,最后再代入特殊值可确定φ的值.(2)先表示出f(α+ ![]() )的表达式,根据tana=2求出cos2a的值代入即可得到答案.
)的表达式,根据tana=2求出cos2a的值代入即可得到答案.


科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上的点且
上的点且![]() 为
为![]() 边
边![]() 上的高.
上的高.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)在线段![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,说出
?若存在,说出![]() 点的位置.
点的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 上关于原点
上关于原点![]() 对称的任意两点,且点
对称的任意两点,且点![]() 都不在
都不在![]() 轴上.
轴上.
(1)若![]() ,求证: 直线
,求证: 直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)若椭圆长轴长为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,设
上,设![]() 是椭圆上异于点
是椭圆上异于点![]() 的任意两点,且
的任意两点,且![]() .问直线
.问直线![]() 是否过一个定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
是否过一个定点?若过定点,求出该定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
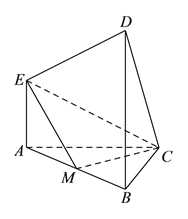
【题目】在如图所示的多面体中, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,且
,且![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .若存在,指出点
.若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某货轮匀速行驶在相距![]() 海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为
海里的甲、乙两地间运输货物,运输成本由燃料费用和其他费用组成.已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为![]() ),其他费用为每小时
),其他费用为每小时![]() 元,且该货轮的最大航行速度为
元,且该货轮的最大航行速度为![]() 海里/小时.
海里/小时.
(1)请将从甲地到乙地的运输成本![]() (元)表示为航行速度
(元)表示为航行速度![]() (海里/小时)的函数;
(海里/小时)的函数;
(2)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解今年高中毕业生的体能状况,从某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.数据分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30 .第6小组的频数是7.
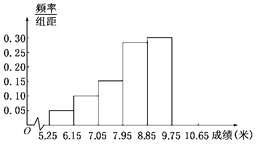
(I)求这次铅球测试成绩合格的人数;
(II)若参加测试的学生中9人成绩优秀,现要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知学生![]() 、
、![]() 的成绩均为优秀,求两人
的成绩均为优秀,求两人![]() 、
、![]() 至少有1人入选的概率.
至少有1人入选的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com