
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)过点
=1(a>b>0)过点 ![]() ,且离心率e为
,且离心率e为 ![]() .
. 
(1)求椭圆E的方程;
(2)设直线x=my﹣1(m∈R)交椭圆E于A,B两点,判断点G ![]() 与以线段AB为直径的圆的位置关系,并说明理由.
与以线段AB为直径的圆的位置关系,并说明理由.
【答案】
(1)解:由已知得 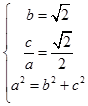 ,解得
,解得 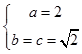 ,
,
∴椭圆E的方程为 ![]()
(2)解:解法一:设点A(x1y1),B(x2,y2),AB中点为H(x0,y0).
由 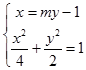 ,化为(m2+2)y2﹣2my﹣3=0,
,化为(m2+2)y2﹣2my﹣3=0,
∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,∴y0=
,∴y0= ![]() .
.
G ![]() ,
,
∴|GH|2= ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]() .
.
![]() =
= ![]() =
= ![]() =
= ![]() ,
,
故|GH|2﹣ ![]() =
= ![]() +
+ ![]() =
= 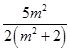 ﹣
﹣ ![]() +
+ ![]() =
= 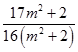 >0.
>0.
∴ ![]() ,故G在以AB为直径的圆外
,故G在以AB为直径的圆外
解法二:设点A(x1y1),B(x2,y2),则 ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
由 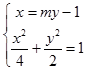 ,化为(m2+2)y2﹣2my﹣3=0,
,化为(m2+2)y2﹣2my﹣3=0,
∴y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,
,
从而 ![]() =
= ![]()
= ![]() +y1y2
+y1y2
= ![]() +
+ ![]()
= 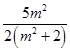 ﹣
﹣ ![]() +
+ ![]() =
= 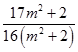 >0.
>0.
∴ ![]() >0,又
>0,又 ![]() ,
, ![]() 不共线,
不共线,
∴∠AGB为锐角.
故点G ![]() 在以AB为直径的圆外
在以AB为直径的圆外
【解析】解法一:(1)由已知得 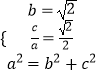 ,解得即可得出椭圆E的方程.(2)设点A(x1,y1),B(x2,y2),AB中点为H(x0,y0).直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,利用根与系数的关系中点坐标公式可得:y0=
,解得即可得出椭圆E的方程.(2)设点A(x1,y1),B(x2,y2),AB中点为H(x0,y0).直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,利用根与系数的关系中点坐标公式可得:y0= ![]() .|GH|2=
.|GH|2= ![]() .
. ![]() =
= ![]() ,作差|GH|2﹣
,作差|GH|2﹣ ![]() 即可判断出.
即可判断出.
解法二:(1)同解法一.(2)设点A(x1,y1),B(x2,y2),则 ![]() =
= ![]() ,
, ![]() =
= ![]() .直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,计算
.直线方程与椭圆方程联立化为(m2+2)y2﹣2my﹣3=0,计算 ![]() =
= ![]() 即可得出∠AGB,进而判断出位置关系.
即可得出∠AGB,进而判断出位置关系.


科目:高中数学 来源: 题型:
【题目】一个公司有8名员工,其中6名员工的月工资分别为5200,5300,5500,6100,6500,6600,另两名员工数据不清楚,那么8位员工月工资的中位数不可能是( )
A.5800
B.6000
C.6200
D.6400
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,f(﹣2)=2021,对任意x∈(﹣∞,+∞),都有f'(x)<2x成立,则不等式f(x)>x2+2017的解集为( )
A.(﹣2,+∞)
B.(﹣2,2)
C.(﹣∞,﹣2)
D.(﹣∞,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数)
(α为参数)
(1)求曲线C的普通方程;
(2)在以O为极点,x正半轴为极轴的极坐标系中,直线l方程为 ![]() ρsin(
ρsin( ![]() ﹣θ)+1=0,已知直线l与曲线C相交于A,B两点,求|AB|.
﹣θ)+1=0,已知直线l与曲线C相交于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的个数是 ①对于命题p:x∈R,使得x2+x+1<0,则p:x∈R,均有x2+x+1>0;
②命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题;
③设ξ~B(n,p),已知Eξ=3,Dξ= ![]() ,则n与p值分别为12,
,则n与p值分别为12, ![]()
④m=3是直线(m+3)x+my﹣2=0与直线mx﹣6y+5=0互相垂直的充要条件.( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(I)讨论函数的单调性,并证明当x>﹣2时,xex+2+x+4>0;
(Ⅱ)证明:当a∈[0,1)时,函数g(x)= ![]() (x>﹣2)有最小值,设g(x)最小值为h(a),求函数h(a)的值域.
(x>﹣2)有最小值,设g(x)最小值为h(a),求函数h(a)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,曲线C1: ![]() (θ为参数),在以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系中,曲线C2:ρsin(
(θ为参数),在以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系中,曲线C2:ρsin( ![]() )=1.
)=1.
(1)求曲线C1的普通方程和曲线C2的直角坐标方程;
(2)曲线C1上恰好存在三个不同的点到曲线C2的距离相等,分别求这三个点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示.

(1)求此几何体的表面积;
(2)如果点![]() 在正视图中所示位置:
在正视图中所示位置:![]() 为所在线段中点,
为所在线段中点,![]() 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从![]() 点到
点到![]() 点的最短路径的长.
点的最短路径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com