
【题目】在△ABC中,D为BC边上的中点,P0是边AB上的一个定点,P0B= ![]() AB,且对于AB上任一点P,恒有
AB,且对于AB上任一点P,恒有 ![]()
![]() ≥
≥ ![]()
![]() ,则下列结论中正确的是(填上所有正确命题的序号).
,则下列结论中正确的是(填上所有正确命题的序号).
①当P与A,B不重合时, ![]() +
+ ![]() 与
与 ![]() 共线;
共线;
② ![]()
![]() =
= ![]() ﹣
﹣ ![]() ;
;
③存在点P,使| ![]() |<|
|<| ![]() |;
|;
④ ![]()
![]() =0;
=0;
⑤AC=BC.
科目:高中数学 来源: 题型:
【题目】已知命题![]() “存在
“存在![]() ”,命题
”,命题![]() :“曲线
:“曲线![]() 表示焦点在
表示焦点在![]() 轴上的椭圆”,命题
轴上的椭圆”,命题![]() “曲线
“曲线![]() 表示双曲线”
表示双曲线”
(1)若“![]() 且
且![]() ”是真命题,求实数
”是真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某城市气象部门的数据中,随机抽取100天的空气质量指数的监测数据如表:
空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200) | (200,300] | (300,+∞) |
质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
天数K | 5 | 23 | 22 | 25 | 15 | 10 |
(1)若该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量![]() (
(![]() 取整数)存在如下关系
取整数)存在如下关系![]() 且当t>300时,y>500,估计在某一医院收治此类病症人数超过200人的概率;
且当t>300时,y>500,估计在某一医院收治此类病症人数超过200人的概率;
(2)若在(1)中,当t>300时,y与t的关系拟合的曲线为![]() ,现已取出了10对样本数据(ti,yi)(i=1,2,3,…,10),且知
,现已取出了10对样本数据(ti,yi)(i=1,2,3,…,10),且知![]()
![]() 试用可线性化的回归方法,求拟合曲线的表达式.(附:线性回归方程
试用可线性化的回归方法,求拟合曲线的表达式.(附:线性回归方程![]() 中,
中, 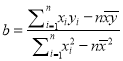 ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() ,若
,若![]() 的图象上相邻两条对称轴的距离为
的图象上相邻两条对称轴的距离为![]() ,图象过点
,图象过点![]() .
.
(1)求![]() 表达式和
表达式和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若函数
的图象,若函数![]() 在区间
在区间![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() ,其中a为常数.
,其中a为常数.
(I)若x=1是函数![]() 的一个极值点,求a的值
的一个极值点,求a的值
(II)若函数![]() 在区间(-1,0)上是增函数,求a的取值范围
在区间(-1,0)上是增函数,求a的取值范围
(III)若函数![]() ,在x=0处取得最大值,求正数a的取值范围
,在x=0处取得最大值,求正数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作,它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个,问该若干?”如图是解决该问题的程序框图,执行该程序框图,求得该垛果子的总数![]() 为( )
为( )

A. 120 B. 84 C. 56 D. 28
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分![]() 分)
分)
已知圆![]() ,过点
,过点![]() 作直线
作直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点.
两点.
(Ⅰ)当![]() 经过圆心
经过圆心![]() 时,求直线
时,求直线![]() 的方程.
的方程.
(Ⅱ)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求弦
时,求弦![]() 的长.
的长.
(Ⅲ)求直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界,已知函数
的上界,已知函数![]() .
.
(Ⅰ)若![]() 是奇函数,求
是奇函数,求![]() 的值.
的值.
(Ⅱ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,判断函数
上的值域,判断函数![]() 在
在![]() 上是否为有界函数,并说明理由.
上是否为有界函数,并说明理由.
(Ⅲ)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的函数,求实数
为上界的函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com