
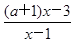 <1.
<1.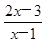 <1,进而可化为
<1,进而可化为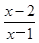 <0(特点:一边为一个分式,另一边为零)可写出不等式的解集; (2)由分式不等式的解法,先将已知不等式化为一边为一个分式,另一边为零的形式:
<0(特点:一边为一个分式,另一边为零)可写出不等式的解集; (2)由分式不等式的解法,先将已知不等式化为一边为一个分式,另一边为零的形式: 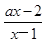 <0
<0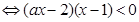 按a=0,a>0和a<0分类讨论,对于a>0,由于方程(ax-2)(x-1)=0的两根为x1=
按a=0,a>0和a<0分类讨论,对于a>0,由于方程(ax-2)(x-1)=0的两根为x1=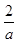 ,x2=1,所以又要按两根的大小分三类:大于、等于和小于进行讨论;对于a<0特别应注意写不等式的解集前先应将字母x的系数化为正.
,x2=1,所以又要按两根的大小分三类:大于、等于和小于进行讨论;对于a<0特别应注意写不等式的解集前先应将字母x的系数化为正.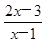 <1,化为
<1,化为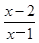 <0, .2分
<0, .2分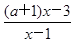 <1得
<1得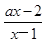 <0, 6分
<0, 6分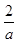 ,x2=1 8分
,x2=1 8分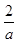 =1即a=2时,解集为
=1即a=2时,解集为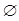 ; .9分
; .9分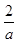 >1即0<a<2时,解集为
>1即0<a<2时,解集为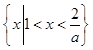 ; 11分
; 11分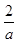 <1即a>2时,解集为
<1即a>2时,解集为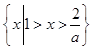 13分
13分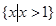
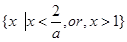


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com