
【题目】如图,某大型厂区有三个值班室![]() ,值班室
,值班室![]() 在值班室
在值班室![]() 的正北方向
的正北方向![]() 千米处,值班室
千米处,值班室![]() 在值班室
在值班室![]() 的正东方向
的正东方向![]() 千米处.
千米处.
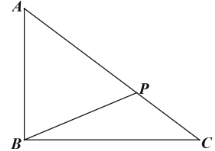
(1)保安甲沿![]() 从值班室
从值班室![]() 出发行至点
出发行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的距离;
的距离;
(2)保安甲沿![]() 从值班室
从值班室![]() 出发前往值班室
出发前往值班室![]() ,保安乙沿
,保安乙沿![]() 从值班室
从值班室![]() 出发前往值班室
出发前往值班室![]() ,甲乙同时出发,甲的速度为
,甲乙同时出发,甲的速度为![]() 千米/小时,乙的速度为
千米/小时,乙的速度为![]() 千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为
千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为![]() 千米(含
千米(含![]() 千米),试问有多长时间两人不能通话?
千米),试问有多长时间两人不能通话?
科目:高中数学 来源: 题型:
【题目】手机运动计步已成为一种时尚,某中学统计了该校教职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
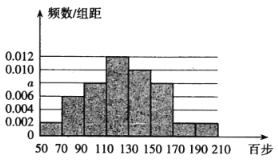
(Ⅰ)求直方图中![]() 的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
(Ⅱ)若该校有教职工175人,试估计一天行走步数不大于130百步的人数;
(Ⅲ)在(Ⅱ)的条件下该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数,
(t为参数,![]() ).在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线
).在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的普通方程;
的普通方程;
(2)若直线l的极坐标方程为![]() ,其中
,其中![]() 满足
满足![]() ,若曲线
,若曲线![]() 和
和![]() 的公共点均在l上,求
的公共点均在l上,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了政府对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房的心理预期调研,用简单随机抽样的方法抽取110人进行统计,得到如下列联表:
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3:8.
![]() 分别求样本中城市人中的不买房人数和农村人中的纠结人数;
分别求样本中城市人中的不买房人数和农村人中的纠结人数;
![]() 用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关?
参考公式:![]() .
.
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,数列
,数列![]() 中的每一项均在集合
中的每一项均在集合![]() 中,且任意两项不相等,又对于任意的整数
中,且任意两项不相等,又对于任意的整数![]() ,均有
,均有![]() .例如
.例如![]() 时,数列
时,数列![]() 为
为![]() 或
或![]() .
.
(1)当![]() 时,试求满足条件的数列
时,试求满足条件的数列![]() 的个数;
的个数;
(2)当![]() ,求所有满足条件的数列
,求所有满足条件的数列![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点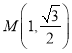 ,
,![]() 的参数方程为
的参数方程为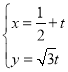 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼奥斯发现:平面上到两定点![]() ,
,![]() 距离之比为常数
距离之比为常数![]() 且
且![]() 的点的轨迹是一个圆心在直线
的点的轨迹是一个圆心在直线![]() 上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体
上的圆,该圆简称为阿氏圆.根据以上信息,解决下面的问题:如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]() ,动点
,动点![]() 满足
满足![]() .若点
.若点![]() 在平面
在平面![]() 内运动,则点
内运动,则点![]() 所形成的阿氏圆的半径为________;若点
所形成的阿氏圆的半径为________;若点![]() 在长方体
在长方体![]() 内部运动,
内部运动,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为
为![]() 的中点,则三棱锥
的中点,则三棱锥![]() 的体积的最小值为___________.
的体积的最小值为___________.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求证:当x∈(0,π]时,f(x)<1;
(2)求证:当m>2时,对任意x0∈(0,π] ,存在x1∈(0,π]和x2∈(0,π](x1≠x2)使g(x1)=g(x2)=f(x0)成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com